题目内容
19.对于任意实数a、b、c、d,我们将式子$\left|\begin{array}{cc}a&b\\ c&d\end{array}\right|$称为二阶行列式,并且规定$\left|\begin{array}{cc}a&b\\ c&d\end{array}\right|=ad-bc$.(1)计算$\left|\begin{array}{cc}2×{10}^{7}&3×{10}^{6}\\ 4×{10}^{6}&7×{10}^{5}\end{array}\right|$的值;
(2)若x2-3x-1=0,求$\left|\begin{array}{cc}x+1&3x\\ x-2&x-1\end{array}\right|$的值.
(3)若n为正整数,试说明$\left|\begin{array}{cc}2n+1&2n-1\\ 2n-1&2n+1\end{array}\right|$的值能被8整除.
分析 (1)原式利用已知的新定义化简,计算即可得到结果;
(2)原式利用已知的新定义化简,把已知等式变形后代入计算即可求出值;
(3)原式利用已知的新定义化简,即可做出判断.
解答 解:(1)根据题意得:原式=2×107×7×105-3×106×4×106=14×1012-12×1012=2×1012;
(2)∵x2-3x-1=0,即x2-3x=1,
∴原式=(x+1)(x-1)-3x(x-2)=-2x2+6x-1=-2(x2-3x)-1=-2×1-1=-3;
(3)原式=(2n+1)2-(2n-1)2=8n,
∵n为正整数,即8n能被8整除
∴$\left|\begin{array}{cc}2n+1&2n-1\\ 2n-1&2n+1\end{array}\right|$的值能被8整除.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
9.二次函数$y=-\frac{1}{2}{({x+3})^2}-2$的顶点坐标是( )
| A. | (3,2) | B. | (3,-2) | C. | (-3,-2) | D. | (-3,2) |
7. 如图,过点A(0,3)的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的表达式是( )
如图,过点A(0,3)的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的表达式是( )
 如图,过点A(0,3)的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的表达式是( )
如图,过点A(0,3)的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的表达式是( )| A. | y=2x+3 | B. | y=x-3 | C. | y=x+3 | D. | y=3-x |
4.两块全等的三角板如图1摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°,BC=1,将图1中的△ABC绕点C顺时针旋转至图2,点P是AC与BA交点,点E是BC上一点,BE⊥BA,则△PBE面积最大值为( )


| A. | 1 | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
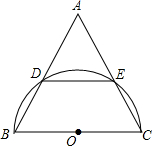 如图,在△ABC中,以BC为直径作半圆O,交AB于点D,交AC于点E,AD=AE.
如图,在△ABC中,以BC为直径作半圆O,交AB于点D,交AC于点E,AD=AE.