题目内容
18．
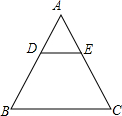如图，在△ABC中，在△ABC中，DE∥BC，若AD：AB=1：3，DE=2，则BC的长为6．
分析 根据DE∥BC，得到△ADE∽△ABC，得到$\frac{AD}{AB}=\frac{DE}{BC}$=$\frac{1}{3}$，即可求BC的长．
解答 解：DE∥BC，
则△ADE∽△ABC，
则$\frac{AD}{AB}=\frac{DE}{BC}$=$\frac{1}{3}$，
∵DE=2，
∴BC=6．
故答案为：6．
点评 本题主要考查相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．
练习册系列答案
小题狂做系列答案
相关题目
8．在平面直角坐标系中，抛物线C1：y=$\frac{1}{2}$x2经过平移得到C2：y=$\frac{1}{2}$x2-2x，则C1平移得到C2的说法正确的是（ ）
| A． | 向左平移2个单位长度 | |
| B． | 向右平移2个单位长度 | |
| C． | 先向左平移2个单位长度，再向下平移2个单位长度 | |
| D． | 先向右平移2个单位长度，再向下平移2个单位长度 |
9．二次函数$y=-\frac{1}{2}{（{x+3}）^2}-2$的顶点坐标是（ ）
| A． | （3，2） | B． | （3，-2） | C． | （-3，-2） | D． | （-3，2） |
7．
如图，过点A（0，3）的一次函数的图象与正比例函数y=2x的图象相交于点B，则这个一次函数的表达式是（ ）
如图，过点A（0，3）的一次函数的图象与正比例函数y=2x的图象相交于点B，则这个一次函数的表达式是（ ）| A． | y=2x+3 | B． | y=x-3 | C． | y=x+3 | D． | y=3-x |
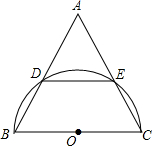如图，在△ABC中，以BC为直径作半圆O，交AB于点D，交AC于点E，AD=AE．