题目内容
2.某校九年级两个班,各选派10名学生参加学校举行的“数学奥林匹克”大赛预赛,各参赛选手的成绩如下:九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
| 班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
| 九(1)班 | 100 | 94 | b | 93 | 12 |
| 九(2)班 | 99 | a | 95.5 | 93 | 8.4 |
(2)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,求另外两个决赛名额落在不同班级的概率.
分析 (1)根据平均数的定义计算(2)班的平均数,根据中位数的定义确定(1)班的中位数;
(2)设九(1)班中98分的两名学生分别用A、B表示,九(2)班中98分的两名学生分别用a、b表示,画树状图展示所有9种等可能的结果数,找出另外两个决赛名额落在不同班级的结果数,然后根据概率公式求解.
解答 解:(1)a=(89+93+93+93+95+96+96+98+98+99)÷10=95(分);
把九(1)派的10名学生的成绩从小到大排列,最中间的两个数的平均数是:$\frac{93+93}{2}$=93,
则中位数b=93;
故答案为:95,93;
(2)设九(1)班中98分的两名学生分别用A、B表示,九(2)班中98分的两名学生分别用a、b表示,
画树状图为:
共有9种等可能的结果数,其中另外两个决赛名额落在不同班级的结果数为8,
所以另外两个决赛名额落在不同班级的概率=$\frac{8}{12}$=$\frac{2}{3}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 完成下面的证明.
完成下面的证明.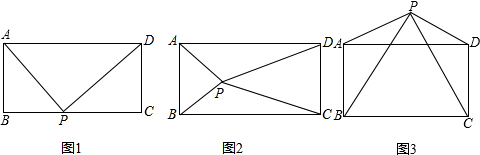
 如图,在网格图中,每格是边长为1的正方形,四边形ABCD的顶点均为格点.
如图,在网格图中,每格是边长为1的正方形,四边形ABCD的顶点均为格点. 如图,现有一架长4m的梯子AB斜靠在墙面上,要想使人安全地攀上梯子的顶端,梯子与地面所成的角α一般要满足50°≤α≤75°.
如图,现有一架长4m的梯子AB斜靠在墙面上,要想使人安全地攀上梯子的顶端,梯子与地面所成的角α一般要满足50°≤α≤75°. 解不等式组$\left\{\begin{array}{l}{1-x>-2①}\\{2x+3≥x-1②}\end{array}\right.$
解不等式组$\left\{\begin{array}{l}{1-x>-2①}\\{2x+3≥x-1②}\end{array}\right.$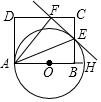 如图,AH是⊙O的直径,矩形ABCD交⊙O于点E,连接AE,将矩形ABCD沿AE折叠,点B落在CD边上的点F处,画直线EF.
如图,AH是⊙O的直径,矩形ABCD交⊙O于点E,连接AE,将矩形ABCD沿AE折叠,点B落在CD边上的点F处,画直线EF.