题目内容
10.林甸某中学开展了一项为贫困学生助学活动,号召学生自愿捐款.已知七年级捐款总额为4800元,八年级捐款总额为5000元,八年级捐款人数比七年级多20人,而且两个年级人均捐款额恰好相等,求两个年级捐款总人数.分析 设出七年级捐款的人数,则可表示出八年级捐款的人数,根据两个年级人均捐款数相等列分式方程求解即可.
解答 解:设七年级捐款的人数为x人,则八年级捐款的人数为(x+20)人.
由题意得:$\frac{4800}{x}$=$\frac{5000}{x+20}$,
解这个方程,得x=480.
经检验,x=480是原方程的解.
则x+x+20=480+480+20=980(人).
答:两个年级捐款总人数为980人.
点评 本题考查分式方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
20.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2.某校九年级两个班,各选派10名学生参加学校举行的“数学奥林匹克”大赛预赛,各参赛选手的成绩如下:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
(1)直接写出表中a、b的值:a=95,b=93;
(2)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,求另外两个决赛名额落在不同班级的概率.
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
| 班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
| 九(1)班 | 100 | 94 | b | 93 | 12 |
| 九(2)班 | 99 | a | 95.5 | 93 | 8.4 |
(2)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,求另外两个决赛名额落在不同班级的概率.
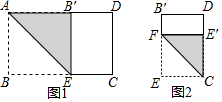 矩形纸片ABCD中,AD=10,AB=a(5<a<10)
矩形纸片ABCD中,AD=10,AB=a(5<a<10)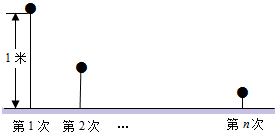 一小球从距地面1m高处自由落下,每次着地后又跳回到原高度的一半再落下.
一小球从距地面1m高处自由落下,每次着地后又跳回到原高度的一半再落下.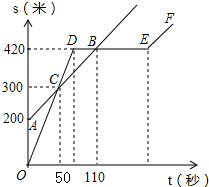 某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动朱老师先跑,当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题:
某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动朱老师先跑,当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题: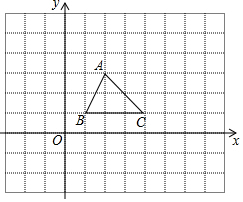 如图,在边长为1个单位长度的小正方形网格中,
如图,在边长为1个单位长度的小正方形网格中,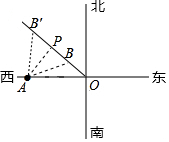 某号台风中心位于O地,台风中心以25km/h的速度向西北方向移动,在距台风中心240km的范围内将受到影响.城市A在O地正西方向与O地相距320km处,如图所示,则A市是否会遭受此台风的影响?若受影响,将有多长时间受影响?($\sqrt{2}$=1.414)
某号台风中心位于O地,台风中心以25km/h的速度向西北方向移动,在距台风中心240km的范围内将受到影响.城市A在O地正西方向与O地相距320km处,如图所示,则A市是否会遭受此台风的影响?若受影响,将有多长时间受影响?($\sqrt{2}$=1.414) 如图,点B、E、C、F在同一条直线上,AB=DE,AB∥DE,BE=CF.求证:AC∥DF.
如图,点B、E、C、F在同一条直线上,AB=DE,AB∥DE,BE=CF.求证:AC∥DF.