题目内容
7. 如图,在网格图中,每格是边长为1的正方形,四边形ABCD的顶点均为格点.
如图,在网格图中,每格是边长为1的正方形,四边形ABCD的顶点均为格点.(1)以O为位似中心,在网格图中作四边形A′B′C′D′,使四边形A′B′C′D′于四边形ABCD位似,且$\frac{OC′}{OC}$=2.
(2)求$\frac{{S}_{△A′B′O}}{{S}_{△A′C′O}}$的值.
分析 (1)利用位似图形的性质得出对应点位置进而得出答案;
(2)分别求出两三角形的面积,即可得出面积之比.
解答 解:(1)如图,四边形A′B′C′D′即为所求;
(2)∵A′B′2=22+22=8、B′O2=42+42=32、A′O2=22+62=40,
∴A′B′2+B′O2=A′O2,
∴△A′B′O是直角三角形,
∴S△A′B′O=$\frac{1}{2}$A′B′×B′O=$\frac{1}{2}$×2$\sqrt{2}$×4$\sqrt{2}$=8,
∵S△A′C′O=$\frac{1}{2}$A′C′×C′O=$\frac{1}{2}$×6×2=6,
∴$\frac{{S}_{△A′B′O}}{{S}_{△A′C′O}}$=$\frac{8}{6}$=$\frac{4}{3}$.
点评 此题主要考查了位似变换的性质,得出对应点位置是解题关键.

练习册系列答案
相关题目
2.某校九年级两个班,各选派10名学生参加学校举行的“数学奥林匹克”大赛预赛,各参赛选手的成绩如下:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
(1)直接写出表中a、b的值:a=95,b=93;
(2)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,求另外两个决赛名额落在不同班级的概率.
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
| 班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
| 九(1)班 | 100 | 94 | b | 93 | 12 |
| 九(2)班 | 99 | a | 95.5 | 93 | 8.4 |
(2)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,求另外两个决赛名额落在不同班级的概率.
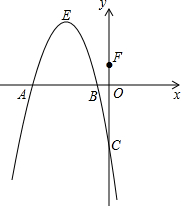 如图,抛物线y=-x2+bx+c交x轴于A,B两点,交y轴于点C,对称轴是直线x=-3,B(-1,0),F(0,1),请解答下列问题:
如图,抛物线y=-x2+bx+c交x轴于A,B两点,交y轴于点C,对称轴是直线x=-3,B(-1,0),F(0,1),请解答下列问题: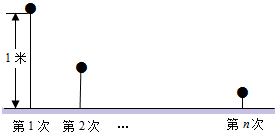 一小球从距地面1m高处自由落下,每次着地后又跳回到原高度的一半再落下.
一小球从距地面1m高处自由落下,每次着地后又跳回到原高度的一半再落下.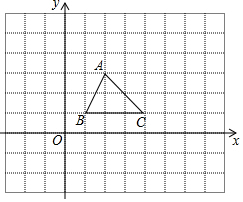 如图,在边长为1个单位长度的小正方形网格中,
如图,在边长为1个单位长度的小正方形网格中,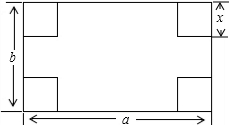 如图,小明想把一长为a,宽为b的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个边长为x的小正方形,用代数式表示纸片剩余部分的周长2a+2b+2x.
如图,小明想把一长为a,宽为b的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个边长为x的小正方形,用代数式表示纸片剩余部分的周长2a+2b+2x.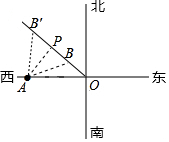 某号台风中心位于O地,台风中心以25km/h的速度向西北方向移动,在距台风中心240km的范围内将受到影响.城市A在O地正西方向与O地相距320km处,如图所示,则A市是否会遭受此台风的影响?若受影响,将有多长时间受影响?($\sqrt{2}$=1.414)
某号台风中心位于O地,台风中心以25km/h的速度向西北方向移动,在距台风中心240km的范围内将受到影响.城市A在O地正西方向与O地相距320km处,如图所示,则A市是否会遭受此台风的影响?若受影响,将有多长时间受影响?($\sqrt{2}$=1.414) 如图,在正方形ABCD外取一点E,连接AE,DE,BE,过点A作AE的垂线交ED于点P,连接BP,AE=AP=1,PB=$\sqrt{5}$,有下列结论:
如图,在正方形ABCD外取一点E,连接AE,DE,BE,过点A作AE的垂线交ED于点P,连接BP,AE=AP=1,PB=$\sqrt{5}$,有下列结论: