题目内容
12.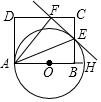 如图,AH是⊙O的直径,矩形ABCD交⊙O于点E,连接AE,将矩形ABCD沿AE折叠,点B落在CD边上的点F处,画直线EF.
如图,AH是⊙O的直径,矩形ABCD交⊙O于点E,连接AE,将矩形ABCD沿AE折叠,点B落在CD边上的点F处,画直线EF.(1)求证:直线EF是⊙O的切线.
(2)若CD=10,EB=5,求⊙O的直径.
分析 (1)连接OE,由折叠的性质结合条件可证得OE∥AF,再由条件可得AF⊥EF,则可证得结论;
(2)可设OA=OE=x,则OB=10-x,在Rt△OBE中,可求得x的值,进一步可求得⊙O的直径.
解答 (1)证明:
如图,连接OE,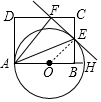
∵OA=OE,
∴∠EAO=∠AEO,
由折叠可得∠EAO=∠FAE,
∴∠FAE=∠AEO,
∴AF∥OE,
∴∠AFE+∠OEF=180°,
在矩形ABCD中,∠ABC=90°,
由折叠可知∠AFE=∠ABC=90°,
∴∠OEF=90°,
∴OE⊥EF,且点E在圆上,OE为半径,
∴EF是⊙O的切线;
(2)解:
∵四边形ABCD是矩形,CD=10,
∴AB=CD=10,∠ABE=90°,
设OA=OE=x,则OB=10-x,
在Rt△OBE中,∠OBE=90°,EB=5,
由勾股定理可得OB2+BE2=OE2,
∴(10-x)2+52=x2,解得x=$\frac{25}{4}$,
∴AH=2x=$\frac{25}{2}$,
∴⊙O的直径为$\frac{25}{2}$.
点评 本题主要考查切线的判定和性质及折叠的性质,掌握切线的两种证明方法是解题的关键,在折叠中求有关线段长度时注意方程思想的应用.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
2.某校九年级两个班,各选派10名学生参加学校举行的“数学奥林匹克”大赛预赛,各参赛选手的成绩如下:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
(1)直接写出表中a、b的值:a=95,b=93;
(2)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,求另外两个决赛名额落在不同班级的概率.
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
| 班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
| 九(1)班 | 100 | 94 | b | 93 | 12 |
| 九(2)班 | 99 | a | 95.5 | 93 | 8.4 |
(2)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,求另外两个决赛名额落在不同班级的概率.
3.在一个不透明的袋中装有2个黄球和2个红球,它们除颜色外没有其他区别,从袋中任意摸出一个球,然后放回搅匀,再从袋中任意摸出一个球,那么两次都摸到黄球的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
 如图,点B、E、C、F在同一条直线上,AB=DE,AB∥DE,BE=CF.求证:AC∥DF.
如图,点B、E、C、F在同一条直线上,AB=DE,AB∥DE,BE=CF.求证:AC∥DF.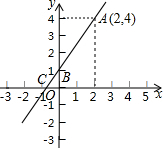 如图,一次函数y=ax+b的图象经过A、B两点,与x轴交于点C.
如图,一次函数y=ax+b的图象经过A、B两点,与x轴交于点C.