题目内容
7.解方程:$\sqrt{2x+1}+\sqrt{x}=1$.分析 先把$\sqrt{x}$移到等号的右边,再两边进行平方,然后合并同类项,得出x+2$\sqrt{x}$=0,再根据二次根式有意义的条件即可得出x的值.
解答 解:∵$\sqrt{2x+1}+\sqrt{x}=1$,
∴$\sqrt{2x+1}$=1-$\sqrt{x}$,
∴($\sqrt{2x+1}$)2=(1-$\sqrt{x}$)2,
∴2x+1=1-2$\sqrt{x}$+x,
∴2x-x+2$\sqrt{x}$=0,
∴x+2$\sqrt{x}$=0,
∵要使式子有意义,x的取值一定是大于等于0,
∵x+2$\sqrt{x}$=0,
∴x=0.
点评 此题考查了无理方程,在解无理方程是最常用的方法是两边平方法及换元法,本题用平方法求出x+2$\sqrt{x}$=0,再x的取值范围求出x的值是本题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
16.下列分解因式中,正确的是( )
| A. | 2x2y-xy2+xy=xy(2x-y) | B. | (x+4y)2-(2x)2=(x+4y+2x)(x+4y-2x) | ||
| C. | x3-2x2+x=x(x-1)2 | D. | 1-4x2y2=(1+4xy)(1-4xy) |
 如图,AD是∠BAC的平分线,点E在BC上,点F在CA的延长线上,EF∥AD交AB于点G,那么图中与∠F相等的角的个数有( )
如图,AD是∠BAC的平分线,点E在BC上,点F在CA的延长线上,EF∥AD交AB于点G,那么图中与∠F相等的角的个数有( )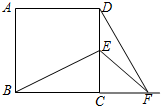 已知,如图正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF.
已知,如图正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF.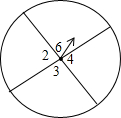 把带有指针的圆形转盘分成4等分,并且在每一区域内标上数字,小红、小明两个人玩转盘游戏,规则是:转动转盘,当转盘停止时,指针指向区域的数字是偶数,则小红胜;若指针指向区域的数字为奇数,则小明胜;若指针落在分割线上,则无效,需重新转动转盘.分别求出小红、小明获胜的概率.
把带有指针的圆形转盘分成4等分,并且在每一区域内标上数字,小红、小明两个人玩转盘游戏,规则是:转动转盘,当转盘停止时,指针指向区域的数字是偶数,则小红胜;若指针指向区域的数字为奇数,则小明胜;若指针落在分割线上,则无效,需重新转动转盘.分别求出小红、小明获胜的概率. Rt△ABC中,∠ACB=90°,AD=4,BD=2,过点C作CD⊥AB,垂足为D.
Rt△ABC中,∠ACB=90°,AD=4,BD=2,过点C作CD⊥AB,垂足为D.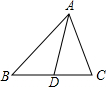 如图,在△ABC中,AD为BC边上的中线,若AB=5,AC=3,则AD的取值范围是1<AD<4.
如图,在△ABC中,AD为BC边上的中线,若AB=5,AC=3,则AD的取值范围是1<AD<4.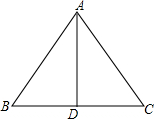 如图,在△ABC中,AB=AC,∠BAC的平分线交BC边于点D,AB=13,BC=10,则AD=12.
如图,在△ABC中,AB=AC,∠BAC的平分线交BC边于点D,AB=13,BC=10,则AD=12.