题目内容
 如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4-x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.
如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4-x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.(1)求抛物线的表达式;
(2)点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;
(3)若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中△AOC与△OBD重叠部分的面积记为S,试求S的最大值.
考点:二次函数综合题,平行四边形的判定与性质,坐标与图形变化-平移
专题:代数几何综合题,压轴题,待定系数法
分析:(1)利用待定系数法求出抛物线的解析式;
(2)由题意,可知MN∥AC,因为以A、C、M、N为顶点的四边形为平行四边形,则有MN=AC=3.设点M的横坐标为x,则求出MN=|
x2-4x|;解方程|
x2-4x|=3,求出x的值,即点M横坐标的值;
(3)设水平方向的平移距离为t(0≤t<2),利用平移性质求出S的表达式:S=-
(t-1)2+
;当t=1时,s有最大值为
.
(2)由题意,可知MN∥AC,因为以A、C、M、N为顶点的四边形为平行四边形,则有MN=AC=3.设点M的横坐标为x,则求出MN=|
| 4 |
| 3 |
| 4 |
| 3 |
(3)设水平方向的平移距离为t(0≤t<2),利用平移性质求出S的表达式:S=-
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:(1)由题意,可得C(1,3),D(3,1).
∵抛物线过原点,∴设抛物线的解析式为:y=ax2+bx.
∴
,
解得
,
∴抛物线的表达式为:y=-
x2+
x.
(2)存在.
设直线OD解析式为y=kx,将D(3,1)代入,
求得k=
,
∴直线OD解析式为y=
x.
设点M的横坐标为x,则M(x,
x),N(x,-
x2+
x),
∴MN=|yM-yN|=|
x-(-
x2+
x)|=|
x2-4x|.
由题意,可知MN∥AC,因为以A、C、M、N为顶点的四边形为平行四边形,则有MN=AC=3.
∴|
x2-4x|=3.
若
x2-4x=3,整理得:4x2-12x-9=0,
解得:x=
或x=
;
若
x2-4x=-3,整理得:4x2-12x+9=0,
解得:x=
.
∴存在满足条件的点M,点M的横坐标为:
或
或
.
(3)∵C(1,3),D(3,1)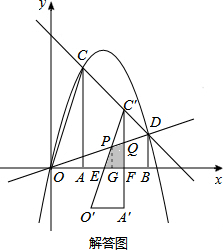
∴易得直线OC的解析式为y=3x,直线OD的解析式为y=
x.
如解答图所示,
设平移中的三角形为△A′O′C′,点C′在线段CD上.
设O′C′与x轴交于点E,与直线OD交于点P;
设A′C′与x轴交于点F,与直线OD交于点Q.
设水平方向的平移距离为t(0≤t<2),
则图中AF=t,F(1+t,0),Q(1+t,
+
t),C′(1+t,3-t).
设直线O′C′的解析式为y=3x+b,
将C′(1+t,3-t)代入得:b=-4t,
∴直线O′C′的解析式为y=3x-4t.
∴E(
t,0).
联立y=3x-4t与y=
x,解得x=
t,
∴P(
t,
t).
过点P作PG⊥x轴于点G,则PG=
t.
∴S=S△OFQ-S△OEP=
OF•FQ-
OE•PG
=
(1+t)(
+
t)-
•
t•
t
=-
(t-1)2+
当t=1时,S有最大值为
.
∴S的最大值为
.
∵抛物线过原点,∴设抛物线的解析式为:y=ax2+bx.
∴
|
解得
|
∴抛物线的表达式为:y=-
| 4 |
| 3 |
| 13 |
| 3 |
(2)存在.
设直线OD解析式为y=kx,将D(3,1)代入,
求得k=
| 1 |
| 3 |
∴直线OD解析式为y=
| 1 |
| 3 |
设点M的横坐标为x,则M(x,
| 1 |
| 3 |
| 4 |
| 3 |
| 13 |
| 3 |
∴MN=|yM-yN|=|
| 1 |
| 3 |
| 4 |
| 3 |
| 13 |
| 3 |
| 4 |
| 3 |
由题意,可知MN∥AC,因为以A、C、M、N为顶点的四边形为平行四边形,则有MN=AC=3.
∴|
| 4 |
| 3 |
若
| 4 |
| 3 |
解得:x=
3+3
| ||
| 2 |
3-3
| ||
| 2 |
若
| 4 |
| 3 |
解得:x=
| 3 |
| 2 |
∴存在满足条件的点M,点M的横坐标为:
| 3 |
| 2 |
3+3
| ||
| 2 |
3-3
| ||
| 2 |
(3)∵C(1,3),D(3,1)

∴易得直线OC的解析式为y=3x,直线OD的解析式为y=
| 1 |
| 3 |
如解答图所示,
设平移中的三角形为△A′O′C′,点C′在线段CD上.
设O′C′与x轴交于点E,与直线OD交于点P;
设A′C′与x轴交于点F,与直线OD交于点Q.
设水平方向的平移距离为t(0≤t<2),
则图中AF=t,F(1+t,0),Q(1+t,
| 1 |
| 3 |
| 1 |
| 3 |
设直线O′C′的解析式为y=3x+b,
将C′(1+t,3-t)代入得:b=-4t,
∴直线O′C′的解析式为y=3x-4t.
∴E(
| 4 |
| 3 |
联立y=3x-4t与y=
| 1 |
| 3 |
| 3 |
| 2 |
∴P(
| 3 |
| 2 |
| 1 |
| 2 |
过点P作PG⊥x轴于点G,则PG=
| 1 |
| 2 |
∴S=S△OFQ-S△OEP=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
=-
| 1 |
| 6 |
| 1 |
| 3 |
当t=1时,S有最大值为
| 1 |
| 3 |
∴S的最大值为
| 1 |
| 3 |
点评:本题是二次函数压轴题,综合考查了二次函数的图象与性质、待定系数法、函数图象上点的坐标特征、平行四边形、平移变换、图形面积计算等知识点,有一定的难度.第(2)问中,解题关键是根据平行四边形定义,得到MN=AC=3,由此列出方程求解;第(3)问中,解题关键是求出S的表达式,注意图形面积的计算方法.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
若
与1互为相反数,则x等于( )
| 2 |
| x-1 |
| A、-1 | B、1 | C、2 | D、3 |
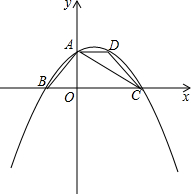 如图,在平面直角坐标系中,四边形ABCD是等腰梯形,AD∥BC,AB=DC,BC在x轴上,点A在y轴的正半轴上,点A,D的坐标分别为A(0,2),D(2,2),AB=2
如图,在平面直角坐标系中,四边形ABCD是等腰梯形,AD∥BC,AB=DC,BC在x轴上,点A在y轴的正半轴上,点A,D的坐标分别为A(0,2),D(2,2),AB=2
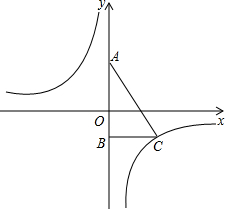 如图,直角三角形ABC,点A的坐标为(0,2),点B的坐标为(0,-2),BC的长为3,反比例函数y=
如图,直角三角形ABC,点A的坐标为(0,2),点B的坐标为(0,-2),BC的长为3,反比例函数y=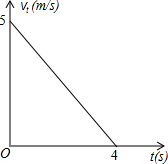 一个小球以初始速度v0=5m/s运动,并且均匀减速,4s后停止运动,下图是运动时间t(s)与第t秒末的速度vt(m/s)的函数图象,下表是小球t秒内所走的路与时间的一些数据:
一个小球以初始速度v0=5m/s运动,并且均匀减速,4s后停止运动,下图是运动时间t(s)与第t秒末的速度vt(m/s)的函数图象,下表是小球t秒内所走的路与时间的一些数据: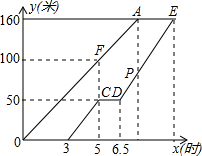 如图,甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数为折线BC-CD-DE,如图,从甲队开始工作时计时.当甲队清理完路面时,乙队铺设完的路面长为
如图,甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数为折线BC-CD-DE,如图,从甲队开始工作时计时.当甲队清理完路面时,乙队铺设完的路面长为