题目内容
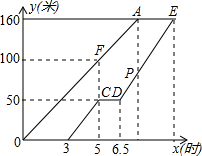 如图,甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数为折线BC-CD-DE,如图,从甲队开始工作时计时.当甲队清理完路面时,乙队铺设完的路面长为
如图,甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数为折线BC-CD-DE,如图,从甲队开始工作时计时.当甲队清理完路面时,乙队铺设完的路面长为考点:一次函数的应用
专题:
分析:先根据函数图象可以得出甲队的工作效率,就可以求出甲队的工作时间,再由待定系数法求出DE的解析式,就可以由自变量的值求出结论.
解答:解:由题意,得
甲队的工作效率为:100÷5=20米,
∴甲队完成的时间为:160÷20=8小时.
乙队的工作效率为:50÷5=10米,
设DE的解析式为y=10x+b,由题意得
50=10×6.5+b,
解得:b=-15.
∴y=10x-15.
当x=8时,
∴y=10×8-15=65.
故答案为:65.
甲队的工作效率为:100÷5=20米,
∴甲队完成的时间为:160÷20=8小时.
乙队的工作效率为:50÷5=10米,
设DE的解析式为y=10x+b,由题意得
50=10×6.5+b,
解得:b=-15.
∴y=10x-15.
当x=8时,
∴y=10×8-15=65.
故答案为:65.
点评:本题考查了待定系数法求一次函数的解析式的运用,工程问题的数量关系的运用,由自变量的值求函数值的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
 如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.
如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE. 如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4-x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.
如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4-x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点. 如图,在Rt△ABC中,AC=3,BC=4,D为斜边AB上的一动点,DE⊥BC,DF⊥AC,垂足为E、F,当线段EF的长最小时,cos∠EFD=
如图,在Rt△ABC中,AC=3,BC=4,D为斜边AB上的一动点,DE⊥BC,DF⊥AC,垂足为E、F,当线段EF的长最小时,cos∠EFD=