题目内容
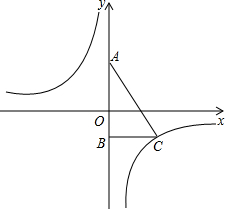 如图,直角三角形ABC,点A的坐标为(0,2),点B的坐标为(0,-2),BC的长为3,反比例函数y=
如图,直角三角形ABC,点A的坐标为(0,2),点B的坐标为(0,-2),BC的长为3,反比例函数y=| k |
| x |
(1)求反比例函数与直经AC的解析式;
(2)点P是反比例函数图象上的点,若使△OAP的面积恰好等于△ABC的面积,求P点的坐标.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)求出C的坐标,代入反比例函数的解析式,即可求出反比例函数的解析式,设直线AC的解析式是y=ax+b,把A、C的坐标代入即可求出直线AC的解析式;
(2)设P的坐标是(x,y),根据三角形面积求出x的值,代入反比例函数的解析式,求出y即可.
(2)设P的坐标是(x,y),根据三角形面积求出x的值,代入反比例函数的解析式,求出y即可.
解答:解:(1)∵点A的坐标为(0,2),点B的坐标为(0,-2),
∴AB=4,
∵BC的长是3,
∴C点的坐标是(3,-2),
∵反比例函数y=
的图象经过点C,
∴k=3×(-2)=-6,
∴反比例函数的解析式是y=-
;
设直线AC的解析式是y=ax+b,
把A(0,2),C(3,-2)代入得:
,
解得:b=2,k=-
,
即直线AC的解析式是y=-
x+2;
(2)设P的坐标是(x,y),
∵△OAP的面积恰好等于△ABC的面积,
∴
×OA•|x|=
×3×4,
解得:x=±6,
∵P点在反比例函数y=-
上,
∴当x=6时,y=-1;
当x=-6时,y=1;
即P点的坐标为(6,-1)或(-6,1).
∴AB=4,
∵BC的长是3,
∴C点的坐标是(3,-2),
∵反比例函数y=
| k |
| x |
∴k=3×(-2)=-6,
∴反比例函数的解析式是y=-
| 6 |
| x |
设直线AC的解析式是y=ax+b,
把A(0,2),C(3,-2)代入得:
|
解得:b=2,k=-
| 4 |
| 3 |
即直线AC的解析式是y=-
| 4 |
| 3 |
(2)设P的坐标是(x,y),
∵△OAP的面积恰好等于△ABC的面积,
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得:x=±6,
∵P点在反比例函数y=-
| 6 |
| x |
∴当x=6时,y=-1;
当x=-6时,y=1;
即P点的坐标为(6,-1)或(-6,1).
点评:本题考查了三角形的面积,用待定系数法求一次函数、反比例函数的解析式的应用,主要考查学生的推理和计算能力,题目比较好,难度适中.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
a为任意实数,点 P(a,a-2)一定不在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4-x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.
如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4-x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.