Question

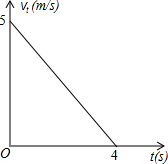一个小球以初始速度v₀=5m/s运动，并且均匀减速，4s后停止运动，下图是运动时间t（s）与第t秒末的速度v_t（m/s）的函数图象，下表是小球t秒内所走的路与时间的一些数据：

时间t（s）	0	1	2	3	4
路程（m）	0	4.375	7.5	9.375	10

（1）求v_t与t的函数关系式，并求t的取值范围
（2）求t秒内小球所走的路程S的函数关系式和S的最大距离．
（3）若行驶的路程不小于7.5m，试根据s与t的图象，求小球运动的时间段．

Answer 1

考点：一次函数的应用

专题：

分析：（1）设v_t与t的函数关系式为v_t=kt+b，由待定系数法求出其解即可；
（2）先求出平均速度，由路程=速度×时间就可以得出结论；
（3）将s=7.5代入（2）的解析式求出其解即可．

解答：解：（1）设v_t与t的函数关系式为v_t=kt+b，由题意，得

5=b 0=4k+b

，
解得：

k=- 5 4 b=5

，
V_t=-

5

4

t+5（0≤t≤4）
（2）由题意，得
t秒时速度为5-

5

4

t，
∴平均速度为：

5+5- 5 4 t

2

=5-

5

8

t，
∴S=（5-

5

8

t）t，
=-

5

8

（t-4）²+10
∴t=4时，S_最大=10；
（3）当s=7.5时，
7.5=-

5

8

（t-4）²+10
∴t₁=2，t₂=6（舍去）
∴2≤t≤4．
答：行驶的路程不小于7.5m时，小球运动的时间段为2≤t≤4．

点评：本题考查了匀减速运动的性质的运用，待定系数法求一次函数的接线上的运用，行程问题的数量关系的运用，一元二次方程的解法的运用，解答时求出平均速度是关键．