题目内容
9.若关于x的一元二次方程(m-2)x2+5x+m2-m-2=0有一个根为0,则m=-1,另一根为$\frac{5}{3}$.分析 将x=0代入原方程求出m值,结合一元二次方程的定义确定m值,再根据根与系数的关系结合方程一根为0即可求出另一根.
解答 解:当x=0时,有m2-m-2=0,
解得:m1=-1,m2=2,
∵原方程为一元二次方程,
∴m-2≠0,
∴m=-1.
当m=-1时,原方程为-3x2+5x=0,
∴方程的另一根为-$\frac{5}{-3}$-0=$\frac{5}{3}$.
故答案为:-1;$\frac{5}{3}$.
点评 本题考查了根与系数的关系以及一元二次方程的解,将x=0代入方程求出m值是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
19.不等式组$\left\{\begin{array}{l}{1-x<2}\\{2x≤6}\end{array}\right.$的解集为( )
| A. | x>-1 | B. | x≤3 | C. | 1<x≤3 | D. | -1<x≤3 |
17.已知x=y,字母m可以取任意有理数,下列等式不一定成立的是( )
| A. | x+m=y+m | B. | x-m=y-m | C. | xm=ym | D. | x+m=x-m |
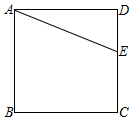 如图,点E是正方形ABCD的边CD上一点,把线段AE沿EC方向平移,使得点E与点C重合,得到线段CF.
如图,点E是正方形ABCD的边CD上一点,把线段AE沿EC方向平移,使得点E与点C重合,得到线段CF.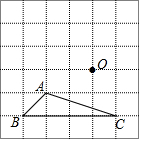 如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上)
如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上)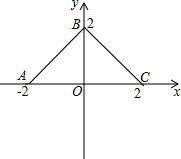 如图,在直角坐标系上有折线段ABC,它们的坐标分别是A(-2,0),B(0,2),C(2,0),若有动直线l:y=t(0<t<2)线段AB交于M,与线段BC交于N,如果记三角形MNO的面积为S.
如图,在直角坐标系上有折线段ABC,它们的坐标分别是A(-2,0),B(0,2),C(2,0),若有动直线l:y=t(0<t<2)线段AB交于M,与线段BC交于N,如果记三角形MNO的面积为S.