题目内容
20.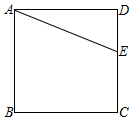 如图,点E是正方形ABCD的边CD上一点,把线段AE沿EC方向平移,使得点E与点C重合,得到线段CF.
如图,点E是正方形ABCD的边CD上一点,把线段AE沿EC方向平移,使得点E与点C重合,得到线段CF.(1)在图中画出线段CF.
(2)线段AE还可以通过一次的图形变换(轴对称或旋转)得到线段CF吗?试作简要说明.
(3)若AE=13,AD=12,直接写出线段EF的长.
分析 (1)根据平移的条件画出图形即可.
(2)线段AE还可以绕正方形对角线的交点旋转180o得到线段CF;只要证明四边形AECF是平行四边形即可解决问题.
(3)作EH⊥AB于H.则四边形ADEH是矩形,在Rt△EHF中,根据EF=$\sqrt{E{H}^{2}+H{F}^{2}}$,求出EH,HF即可.
解答 解(1)线段CF如图所示,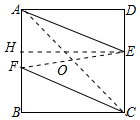
(2)线段AE还可以绕正方形对角线的交点旋转180o得到线段CF;
理由:∵AE=CF,AE∥CF,
∴四边形AECF是平行四边形,连接AC、EF交于点O,
∴OA=OC,
∵四边形AECF是中心对称图形,
∴线段AE还可以绕正方形对角线的交点O旋转180o得到线段CF.
(3)作EH⊥AB于H.则四边形ADEH是矩形,AH=DE=$\sqrt{A{E}^{2}-A{D}^{2}}$=5,EC=AF=7,
在Rt△EHF中,∵EH=AD=12,HF=AF-AH=CE-DE=7-5=2,
∴EF=$\sqrt{E{H}^{2}+H{F}^{2}}$=$\sqrt{1{2}^{2}+{2}^{2}}$=$2\sqrt{37}$.
点评 本题考查正方形的性质、平移变换、旋转变换、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线构造特殊三角形,属于中考常考题型.

练习册系列答案
相关题目
11.若a<0,则下列结论不正确的是( )
| A. | a2=(-a)2 | B. | a3=(-a)3 | C. | a2=|a|2 | D. | a3=-|a|3 |
8.若x=1是一元二次方程x2+2x+m=0的一个根,则m的值为( )
| A. | 3 | B. | -3 | C. | 1 | D. | -1 |
15.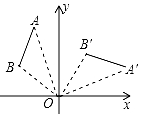 如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )
如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )
 如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )
如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是( )| A. | (5,2) | B. | (2,5) | C. | (2,-5) | D. | (5,-2) |
12. 如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=135°,则∠4的度数为( )
如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=135°,则∠4的度数为( )
 如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=135°,则∠4的度数为( )
如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=135°,则∠4的度数为( )| A. | 55° | B. | 65° | C. | 135° | D. | 45° |
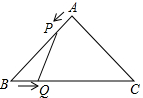 如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t s,四边形APQC的面积为y cm2.
如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t s,四边形APQC的面积为y cm2.