题目内容
17. 如图,AB∥EF,∠C=∠D=85°,CF=BD,若∠A=40°,则∠EFD=55°.
如图,AB∥EF,∠C=∠D=85°,CF=BD,若∠A=40°,则∠EFD=55°.
分析 利用已知条件证明△ABC≌△DFE(ASA),得到∠A=∠E=40°,再利用三角形的内角和为180°,即可解答.
解答 解:∵AB∥EF,
∴∠ABC=∠EFD,
∵CF=BD,
∴CF+BF=BD+BF,
∴BC=DF,
在△ABC和△DFE中,
$\left\{\begin{array}{l}{∠C=∠D}\\{BC=DF}\\{∠ABC=∠EFD}\end{array}\right.$
∴△ABC≌△DFE(ASA),
∴∠A=∠E=40°,
∴∠EFD=180°-∠D-∠E=180°-85°-40°=55°.
点评 本题考查了全等三角形的性质定理与判定定理,解决本题的关键是证明△ABC≌△DFE(ASA).

练习册系列答案
相关题目
8. 判断满足下列关系的两个三角形是否是位似图形?如果是,请指出位似中心.
判断满足下列关系的两个三角形是否是位似图形?如果是,请指出位似中心.
(1)如图(1)所示,AB,CD相交于点O,且∠B=∠D,AD=CB;
(2)如图(2)所示,AB,CD相交于点O,且∠B=∠A.
 判断满足下列关系的两个三角形是否是位似图形?如果是,请指出位似中心.
判断满足下列关系的两个三角形是否是位似图形?如果是,请指出位似中心.(1)如图(1)所示,AB,CD相交于点O,且∠B=∠D,AD=CB;
(2)如图(2)所示,AB,CD相交于点O,且∠B=∠A.
12.关于一次函数y=2x-1,y=-2x+1的图象,下列说法正确的是( )
| A. | 关于直线y=-x对称 | B. | 关于x轴对称 | ||
| C. | 关于y轴对称 | D. | 关于直线y=x对称 |
 如图,小丽想测量学校旗杆的高度,她在地面A点安置侧倾器,测得旗杆顶端C的仰角为30°,侧倾器到旗杆底部的距离AD为12米,侧倾器的高度AB为1.6米,那么旗杆的高度CD为1.6+4$\sqrt{3}$米(保留根号)
如图,小丽想测量学校旗杆的高度,她在地面A点安置侧倾器,测得旗杆顶端C的仰角为30°,侧倾器到旗杆底部的距离AD为12米,侧倾器的高度AB为1.6米,那么旗杆的高度CD为1.6+4$\sqrt{3}$米(保留根号) 如图,反比例函数y=$\frac{6}{x}$(x>0)的图象和矩形ABCD都在第一象限内,AD与x轴平行,已知点A的坐标是(2,6),AB=2,AD=4.现将矩形ABCD向下平移m个单位,要使矩形ABCD与反比例函数y=$\frac{6}{x}$(x>0)的图象有交点,则m的取值范围是1≤m≤5.
如图,反比例函数y=$\frac{6}{x}$(x>0)的图象和矩形ABCD都在第一象限内,AD与x轴平行,已知点A的坐标是(2,6),AB=2,AD=4.现将矩形ABCD向下平移m个单位,要使矩形ABCD与反比例函数y=$\frac{6}{x}$(x>0)的图象有交点,则m的取值范围是1≤m≤5.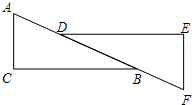 如图,在△ABC与△FDE中,点D在AB上,点B在DF上,∠C=∠E,AC∥FE,AD=FB.求证:△ABC≌△FDE.
如图,在△ABC与△FDE中,点D在AB上,点B在DF上,∠C=∠E,AC∥FE,AD=FB.求证:△ABC≌△FDE.