题目内容
11.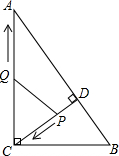 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到点C时,两点都停止.设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到点C时,两点都停止.设运动时间为t秒.(1)求线段CD的长;
(2)当t取何值时PQ∥AB?
(3)是否存在某一时刻t,使得△PCQ为等腰三角形?若存在,求出所有满足条件的t的值;若不存在,请说明理由.
分析 (1)先根据勾股定理求出AB的长,再由三角形的面积公式即可得出结论;
(2)先用t表示出DP,CQ,CP的长,再根据PQ∥AB,得到△QCP∽△ABC,根据相似三角形的性质列方程即可得到结论;
(3)根据题意画出图形,分CQ=CP,PQ=PC,QC=QP三种情况进行讨论.
解答 解:(1)∵∠ACB=90°,AC=8,BC=6,
∴AB=10.
∵CD⊥AB,
∴S△ABC=$\frac{1}{2}$BC•AC=$\frac{1}{2}$AB•CD.
∴CD=$\frac{BC•AC}{AB}$=$\frac{6×8}{10}$=4.8.
∴线段CD的长为4.8.
(2)设DP=t,CQ=t.则CP=4.8-t.
∵PQ∥AB,
∵△QCP∽△ABC
∴$\frac{CQ}{AB}=\frac{CP}{BC}$,即$\frac{t}{10}=\frac{4.8-t}{6}$,
∴t=3,
当t=3时,PQ∥AB;
(3)①若CQ=CP,如图1,
则t=4.8-t.
解得:t=2.4.
②若PQ=PC,如图2所示.
∵PQ=PC,PH⊥QC,
∴QH=CH=$\frac{1}{2}$QC=$\frac{t}{2}$.
∵△CHP∽△BCA.
∴$\frac{CH}{BC}=\frac{CP}{AB}$,
∴$\frac{\frac{t}{2}}{6}$=$\frac{4.8-t}{10}$,解得t=$\frac{144}{55}$;
③若QC=QP,
过点Q作QE⊥CP,垂足为E,如图3所示.
同理可得:t=$\frac{24}{11}$.
综上所述:当t为2.4秒或$\frac{144}{55}$秒或$\frac{24}{11}$秒时,△CPQ为等腰三角形.
点评 本题考查的是相似形综合题,涉及到相似三角形的判定与性质,等腰三角形的判定和性质,三角形的面积的计算,在解答此题时要注意进行分类讨论.

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 我国的“蛟龙号”创造了世界同类潜水器最大下潜深度纪录7062米.如图,
我国的“蛟龙号”创造了世界同类潜水器最大下潜深度纪录7062米.如图,在某次任务中,“蛟龙号”在点A处测得正前方海底沉船C的俯角为45°,然后在同一深度向正前方直线航行600米到点B,此时测得海底沉船C的俯角为60°,那么“蛟龙号”在点B下潜到沉船C处,下潜的垂直深度是( )米.
| A. | 600-600$\sqrt{3}$ | B. | 600+600$\sqrt{3}$ | C. | 900-300$\sqrt{3}$ | D. | 900+300$\sqrt{3}$ |
 如图,在△ABC中,AB=AC,∠A=30°,以C为圆心,CB的长为半径作圆弧,交AB于点D,连接CD,则∠ACD等于( )
如图,在△ABC中,AB=AC,∠A=30°,以C为圆心,CB的长为半径作圆弧,交AB于点D,连接CD,则∠ACD等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
| A. | $-\frac{2}{3}$ | B. | -2 | C. | 2 | D. | $\frac{2}{3}$ |
 如图,反比例函数y=$\frac{6}{x}$(x>0)的图象和矩形ABCD都在第一象限内,AD与x轴平行,已知点A的坐标是(2,6),AB=2,AD=4.现将矩形ABCD向下平移m个单位,要使矩形ABCD与反比例函数y=$\frac{6}{x}$(x>0)的图象有交点,则m的取值范围是1≤m≤5.
如图,反比例函数y=$\frac{6}{x}$(x>0)的图象和矩形ABCD都在第一象限内,AD与x轴平行,已知点A的坐标是(2,6),AB=2,AD=4.现将矩形ABCD向下平移m个单位,要使矩形ABCD与反比例函数y=$\frac{6}{x}$(x>0)的图象有交点,则m的取值范围是1≤m≤5. 已知:如图,AB是⊙O的直径,直线l交⊙O于C、D两点,AE⊥l,BF⊥l,E、F是垂足,求证:EC=DF.
已知:如图,AB是⊙O的直径,直线l交⊙O于C、D两点,AE⊥l,BF⊥l,E、F是垂足,求证:EC=DF. 如图,由射线AB,BC,CD,DA组成平面图形,则∠1+∠2+∠3+∠4=360°.
如图,由射线AB,BC,CD,DA组成平面图形,则∠1+∠2+∠3+∠4=360°. 如图1,已知GF∥BC.
如图1,已知GF∥BC.