题目内容
1.抛物线y=$\frac{1}{2}$x2-2x+$\frac{3}{2}$与x轴的交点坐标是( )| A. | (1,0) | B. | (3,0) | C. | (1,0)或(3,0) | D. | (1,0)或(-3,0) |
分析 要求抛物线与x轴的交点,即令y=0,解方程即可.
解答 解:令y=0,则$\frac{1}{2}$x2-2x+$\frac{3}{2}$=0,
即(x-1)(x-3)=0,
解得x1=1,x2=3,
所以抛物线y=$\frac{1}{2}$x2-2x+$\frac{3}{2}$与x轴的交点的坐标是(1,0)、(3,0).
故选C.
点评 本题考查了抛物线与x轴的交点问题.注意将二次函数y=$\frac{1}{2}$x2-2x+$\frac{3}{2}$与一元二次方程$\frac{1}{2}$x2-2x+$\frac{3}{2}$=0联系起来.

练习册系列答案
相关题目
16.今年,我省启动了“爱护眼睛保护视力”仪式,某小学为了了解各年级戴近视镜的情况,对一到六年级近视的学生进行了统计,得到每个年级的近视的儿童人数分别为20,30,20,34,36,40,对于这组数据,下列说法错误的是( )
| A. | 平均数是30 | B. | 众数是20 | C. | 中位数是34 | D. | 方差是$\frac{176}{3}$ |
12.如果x2+4xy+4y2=0,那么$\frac{x}{y}$的值为( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
16.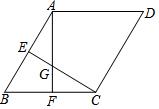 如图,在菱形ABCD中,∠B=60°,E、F分别是AB、BC的中点,CE、AF相交于点G,则四边形AGCD各边中点连线是( )
如图,在菱形ABCD中,∠B=60°,E、F分别是AB、BC的中点,CE、AF相交于点G,则四边形AGCD各边中点连线是( )
 如图,在菱形ABCD中,∠B=60°,E、F分别是AB、BC的中点,CE、AF相交于点G,则四边形AGCD各边中点连线是( )
如图,在菱形ABCD中,∠B=60°,E、F分别是AB、BC的中点,CE、AF相交于点G,则四边形AGCD各边中点连线是( )| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 正方形 |
6. 如图,已知AB∥CD,BC平分∠ABE,∠C=29°,则∠BED的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=29°,则∠BED的度数是( )
 如图,已知AB∥CD,BC平分∠ABE,∠C=29°,则∠BED的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=29°,则∠BED的度数是( )| A. | 18° | B. | 29° | C. | 58° | D. | 38° |
13.已知圆锥的底面半径为3cm,母线长为5cm,则圆锥的侧面积是( )
| A. | 20 cm2 | B. | 20π cm2 | C. | 15 cm2 | D. | 15π cm2 |
10.若最简二次根式$\sqrt{1+2a}$与2$\sqrt{3}$是同类二次根式,则a的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | $\frac{5}{2}$ |
11.某班的一次数学测验中,共出了20道选择题,每小题5分,总分为100分,答对加分,答错倒扣分.现从中抽出5份试卷进行分析,如表:
(1)甲同学得了76分,他答对了多少道题?
(2)有一位同学说“同学乙得了89分”,这个成绩准确吗?为什么?
| 试卷 | 正确个数 | 错误个数 | 得分 |
| A | 19 | 1 | 94 |
| B | 18 | 2 | 88 |
| C | 17 | 3 | 82 |
| D | 14 | 6 | 64 |
| E | 10 | 10 | 40 |
(2)有一位同学说“同学乙得了89分”,这个成绩准确吗?为什么?
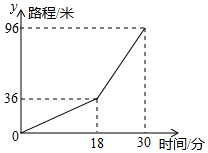 小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.
小亮早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.