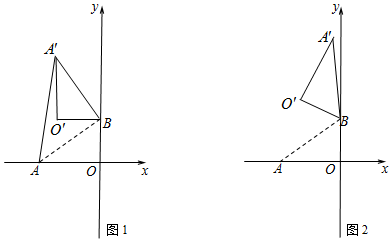
题目内容
15.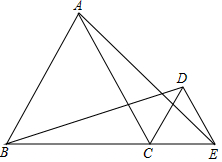 如图,△ABC,△CDE是等边三角形.
如图,△ABC,△CDE是等边三角形.(1)求证:AE=BD;
(2)若BD和AC交于点M,AE和CD交于点N,求证:CM=CN;
(3)连结MN,猜想MN与BE的位置关系.并加以证明.
分析 (1)欲证明AE=BD,只要证明△ACE≌△BCD(SAS)即可.
(2)欲证明CM=CN,只要证明△BCM≌△ACN(ASA)即可.
(3)结论:MN∥BE.只要证明△MNC是等边三角形,即可推出∠CMN=∠BCM,推出MN∥BE.
解答 (1)证明:∵△ABC和△DCE均为等边三角形,
∴AC=BC,CE=CD,∠ACB=∠DCE=60° ,
,
∴∠BCD=∠ACE=120°,
在△ACE和△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CE=CD}\end{array}\right.$,
∴△ACE≌△BCD(SAS)
∴AE=BD.
(2)证明:∵△ACE≌△BCD,
∴∠CBD=∠CAE,
又∵BC=AC,∠BCM=∠ACN=60°,
在△BCN和△ACN中,
$\left\{\begin{array}{l}{∠CBM=∠CAN}\\{CB=CA}\\{∠BCM=∠ACN}\end{array}\right.$,
∴△BCM≌△ACN(ASA)
∴CM=CN
(3)结论:MN∥BE.
理由:∵∠BCA=∠DCE=60°,
∴∠MCN=180°-60°-60°=60°,
∵CM=CN,
∴△CMN是等边三角形,
∴∠CMN=∠BCM=60°,
∴MN∥BE.
点评 本题考查全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
3. 小明家上个月支出共计800元,各项支出如图所示,其中用于教育上的支出是( )
小明家上个月支出共计800元,各项支出如图所示,其中用于教育上的支出是( )
 小明家上个月支出共计800元,各项支出如图所示,其中用于教育上的支出是( )
小明家上个月支出共计800元,各项支出如图所示,其中用于教育上的支出是( )| A. | 232元 | B. | 200元 | C. | 160元 | D. | 80元 |
7.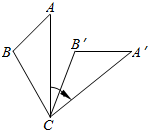 如图,将△ABC绕着点C顺时针旋转45°后得到△A′B′C.若∠A=45°.∠B′=110°,则∠BCA′的度数是( )
如图,将△ABC绕着点C顺时针旋转45°后得到△A′B′C.若∠A=45°.∠B′=110°,则∠BCA′的度数是( )
 如图,将△ABC绕着点C顺时针旋转45°后得到△A′B′C.若∠A=45°.∠B′=110°,则∠BCA′的度数是( )
如图,将△ABC绕着点C顺时针旋转45°后得到△A′B′C.若∠A=45°.∠B′=110°,则∠BCA′的度数是( )| A. | 30° | B. | 70° | C. | 80° | D. | 110° |
 如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为36cm2,则△BEF的面积=9cm2.
如图,点D是△ABC的边BC上任意一点,点E、F分别是线段AD、CE的中点,且△ABC的面积为36cm2,则△BEF的面积=9cm2.