题目内容
12．如图，已知1号、4号两个正方形的面积和为10，2号、3号两个正方形的面积和为7，则a，b，c三个方形的面积和为（ ）
| A． | 17 | B． | 27 | C． | 24 | D． | 34 |
分析 由图可以得到a、b、c三个正方形的面积与1号、2号、3号、4号正方形的面积之间的关系，再根据1号、4号两个正方形的面积和为10，2号、3号两个正方形的面积和为7，可以求得a，b，c三个正方形的面积的和．
解答 解：如下图所示，
∵∠ACB+∠DCE=90°，∠ACB+∠CAB=90°，
∴∠BAC=∠ECD，
在△ABC和△CED中，
$\left\{\begin{array}{l}{∠ABC=∠CED}\\{∠BAC=∠ECD}\\{AC=CD}\end{array}\right.$
∴△ABC≌△CED（AAS）
∴BC=DE，
∵AB2+BC2=AC2，
∴S1+S2=Sa，
同理可证，S2+S3=Sb，S3+S4=Sc，
∴Sa+Sb+Sc=S1+S2+S2+S3+S3+S4，
∵S1+S4=10，S2+S3=7，
∴Sa+Sb+Sc=S1+S2+S2+S3+S3+S4=（S1+S4）+（S2+S3）+（S2+S3）=10+7+7=24，
故选C．
点评 本题考查勾股定理、全等三角形的判定与性质、正方形的性质，解题的关键是利用数形结合的思想解答问题．
练习册系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
2．若点A（2，y1），B（-3，y2），C（-1，y3）三点在抛物线y=x2-4x+5的图象上，则y1、y2、y3的大小关系是（ ）
| A． | y1＞y2＞y3 | B． | y2＞y1＞y3 | C． | y2＞y3＞y1 | D． | y3＞y1＞y2 |
如图，在△ABC中，AE是中线，AD是角平分线，AF是高，∠B=30°，∠C=80°，BE=3，AF=2，填空：
[背景知识]数轴是初中数学的一个重要工具，利用数轴可以将数与形完美的结合．研究数轴我们发现了许多重要的规律：数轴上A点、B点表示的数为a、b，则A，B两点之间的距离AB=|a-b|，若a＞b，则可简化为AB=a-b；线段AB的中点M表示的数为$\frac{a+b}{2}$．
如图，△ABC为等边三角形，D、E分别是AC、BC上的点，且AD=CE，AE与BD相交于点P，
1．
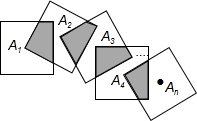如图，将n个边长都为2的正方形按如图所示摆放，点A1，A2，…An分别是正方形的中心，则这n个正方形重叠部分的面积之和是（ ）
如图，将n个边长都为2的正方形按如图所示摆放，点A1，A2，…An分别是正方形的中心，则这n个正方形重叠部分的面积之和是（ ）| A． | n | B． | n-1 | C． | 4（n-1） | D． | 4n |
2．
画函数y=2x+1的图象（先填下表，再在图中的直角坐标系中描点，连线）
画函数y=2x+1的图象（先填下表，再在图中的直角坐标系中描点，连线） | x | -2.5 | -2 | -1 | 0 | 1 | 2 | 2.5 |
| y |