题目内容
1.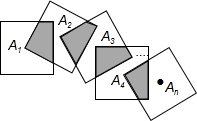 如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )
如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )| A. | n | B. | n-1 | C. | 4(n-1) | D. | 4n |
分析 根据题意可得,阴影部分的面积是正方形的面积的$\frac{1}{4}$,已知两个正方形可得到一个阴影部分,则n个这样的正方形重叠部分即为(n-1)个阴影部分的和.
解答 解:由题意可得一个阴影部分面积等于正方形面积的$\frac{1}{4}$,即是$\frac{1}{4}$×4=1,
n个这样的正方形重叠部分(阴影部分)的面积和为:1×(n-1)=n-1.
故选:B.
点评 此题考查了正方形的性质,解决本题的关键是得到n个这样的正方形重叠部分(阴影部分)的面积和的计算方法,难点是求得一个阴影部分的面积.

练习册系列答案
相关题目
11.点M(-3,2)向上平移2个单位,向下平移3个单位后得点N它的坐标是( )
| A. | (1,1) | B. | (-3,1) | C. | (-1,-1) | D. | (1,-1) |
12.如图,已知1号、4号两个正方形的面积和为10,2号、3号两个正方形的面积和为7,则a,b,c三个方形的面积和为( )


| A. | 17 | B. | 27 | C. | 24 | D. | 34 |
9. 如图,某数学学习兴趣小组为了测量树AB的度数,他们测得此树在阳光下的影子BC的长为9m,在相同时刻,他们还测得小亮在阳光下的影长为1.5m,已知小亮的身高为1.8m,则树AB的高为( )
如图,某数学学习兴趣小组为了测量树AB的度数,他们测得此树在阳光下的影子BC的长为9m,在相同时刻,他们还测得小亮在阳光下的影长为1.5m,已知小亮的身高为1.8m,则树AB的高为( )
 如图,某数学学习兴趣小组为了测量树AB的度数,他们测得此树在阳光下的影子BC的长为9m,在相同时刻,他们还测得小亮在阳光下的影长为1.5m,已知小亮的身高为1.8m,则树AB的高为( )
如图,某数学学习兴趣小组为了测量树AB的度数,他们测得此树在阳光下的影子BC的长为9m,在相同时刻,他们还测得小亮在阳光下的影长为1.5m,已知小亮的身高为1.8m,则树AB的高为( )| A. | 10.8m | B. | 9m | C. | 7.5m | D. | 0.3m |
10. 如图所示,河堤横断面堤高BC=$5\sqrt{3}$米,迎水坡面AB的坡度为$\frac{{\sqrt{3}}}{3}$(坡度是指坡面的铅直高度与水平宽度之比,又称坡比),则AC的长是( )
如图所示,河堤横断面堤高BC=$5\sqrt{3}$米,迎水坡面AB的坡度为$\frac{{\sqrt{3}}}{3}$(坡度是指坡面的铅直高度与水平宽度之比,又称坡比),则AC的长是( )
 如图所示,河堤横断面堤高BC=$5\sqrt{3}$米,迎水坡面AB的坡度为$\frac{{\sqrt{3}}}{3}$(坡度是指坡面的铅直高度与水平宽度之比,又称坡比),则AC的长是( )
如图所示,河堤横断面堤高BC=$5\sqrt{3}$米,迎水坡面AB的坡度为$\frac{{\sqrt{3}}}{3}$(坡度是指坡面的铅直高度与水平宽度之比,又称坡比),则AC的长是( )| A. | $5\sqrt{3}$米 | B. | 10米 | C. | 15米 | D. | 10$\sqrt{3}$米 |
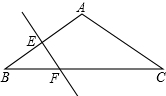 如图:△ABC中,AB=AC.∠BAC=120°,EF垂直平分AB,EF=2,求AB与BC的长.
如图:△ABC中,AB=AC.∠BAC=120°,EF垂直平分AB,EF=2,求AB与BC的长. 如图,AB=DC,AC=DB,由此你能猜想出什么结论?并简要说明理由.
如图,AB=DC,AC=DB,由此你能猜想出什么结论?并简要说明理由.