题目内容
4. 如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,
如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,(1)求∠BPE的度数;
(2)若BF⊥AE于点F,试判断BP与PF的数量关系.
分析 (1)由等边三角形的性质得出AB=CA,∠BAD=∠ACE=60°,由SAS即可证明△ABD≌△CAE,得到∠ABD=∠CAE,利用外角∠BPE=∠BAP+∠ABD,即可解答
(2)由△ABD≌△CAE得出对应角相等∠ABD=∠CAE,根据三角形的外角性质得出∠BPF=60°,由含30°角的直角三角形的性质即可得出PF与BP的关系.
解答 解:(1)∵△ABC是等边三角形,
∴AB=CA,∠BAD=∠ACE=60°,
在△ABD和△CAE中,
$\left\{\begin{array}{l}{AB=CA}\\{∠BAD=∠ACE}\\{AD=CE}\end{array}\right.$,
∴△ABD≌△CAE(SAS),
∴∠ABD=∠CAE,
∵∠BPE=∠BAP+∠ABD,
∴∠BPE=∠BAP+∠CAE=∠BAC=60°.
(2)PF=$\frac{1}{2}$BP.
∵△ABD≌△CAE,
∴∠ABD=∠CAE,
∵∠BPF=∠BAP+∠ABD,
∴∠BPF=∠BAP+∠CAE=∠BAD=60°,
∵BF⊥AE,
∴∠PFB=90°,
∴∠PBF=30°,
∴PF=$\frac{1}{2}$BP.
点评 本题考查了等边三角形的性质、全等三角形的判定与性质、含30°角的直角三角形的性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
14.下列算式能用平方差公式计算的是( )
| A. | (3a+b)(3b-a) | B. | (a+b)(a-b) | C. | (2x-y)(-2x+y) | D. | (m+n)(-m-n) |
15.下列事件中必然发生的事件是( )
| A. | 一个图形平移后所得的图形与原来的图形不全等 | |
| B. | 100件产品中有4件次品,从中任意抽取5件,至少一件是正品 | |
| C. | 不等式的两边同时乘以一个数,结果仍是不等式 | |
| D. | 随意翻一本书的某页,这页的页码一定是偶数 |
12.如图,已知1号、4号两个正方形的面积和为10,2号、3号两个正方形的面积和为7,则a,b,c三个方形的面积和为( )


| A. | 17 | B. | 27 | C. | 24 | D. | 34 |
 如图,水平放置的圆柱形排水管的截面半径为10cm,截面中有水部分弓形高为5cm,则水面宽AB为10$\sqrt{3}$cm.
如图,水平放置的圆柱形排水管的截面半径为10cm,截面中有水部分弓形高为5cm,则水面宽AB为10$\sqrt{3}$cm. 如图,某数学学习兴趣小组为了测量树AB的度数,他们测得此树在阳光下的影子BC的长为9m,在相同时刻,他们还测得小亮在阳光下的影长为1.5m,已知小亮的身高为1.8m,则树AB的高为( )
如图,某数学学习兴趣小组为了测量树AB的度数,他们测得此树在阳光下的影子BC的长为9m,在相同时刻,他们还测得小亮在阳光下的影长为1.5m,已知小亮的身高为1.8m,则树AB的高为( )
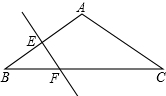 如图:△ABC中,AB=AC.∠BAC=120°,EF垂直平分AB,EF=2,求AB与BC的长.
如图:△ABC中,AB=AC.∠BAC=120°,EF垂直平分AB,EF=2,求AB与BC的长. 如图,二次函数y=-x2-(2m+2)x-m2-4m+3(m为非负整数)与x轴交于A、B两点,与y轴交于C点.
如图,二次函数y=-x2-(2m+2)x-m2-4m+3(m为非负整数)与x轴交于A、B两点,与y轴交于C点.