题目内容

12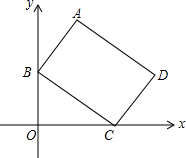．如图，?ABCD的顶点C，B分别在x轴，y轴上，顶点A，D的坐标分别为（2，4），（5，2），则顶点B，C的坐标分别是（0，2）、（3，0）．

分析 结合平行四边形的对边相等的性质来求顶点B，C的坐标．

解答 解：依题意得：yA-yB=yD-yC，即4-yB=2-0，故yB=2．所以B（0，2）．
xA-xB=xD-xC，即2-0=5-xC，故xC=3．所以C（3，0）．
故答案是：（0，2）、（3，0）．

点评 本题考查了平行四边形的性质，坐标与图形性质，根据图形得到点A、D与点B、C的坐标间的数量关系是解题的关键．

练习册系列答案
相关题目
2．已知关于x、y的方程组$\left\{\begin{array}{l}{x+y=6m}\\{x-y=10m}\end{array}\right.$也满足2x-3y=11，则m的值等于（　　）
A．-$\frac{1}{2}$B．$\frac{1}{2}$C．$\frac{28}{11}$D．-$\frac{28}{11}$
3．若方程mx+ny=6的两个解是$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$，$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$，则m，n的值为m=4.5，n=1.5．
20．如图，AB∥CD，∠CDE=110°，GF交∠DEB的平分线EF于点EF，∠AGF=130°，则∠F=（　　）
A．4°B．5°C．6°D．10°
7．若一元二次方程ax2-bx-2016=0满足a+b=2016，则此方程必有一根为x=-1．
17．在?ABCD中，AB=3，BC=5，AC=4，则AD，BC间的距离等于$\frac{12}{5}$．
4．在?ABCD中，∠A=110°，则∠D=70°．
1．已知方程2x+y-4=0，当x与y互为相反数时，则x=4．
2．若关于x的一元二次方程（a-1）x2-2x+2=0有实数根，则整数a的最大值为（　　）
A．0B．1C．2D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网