题目内容
2.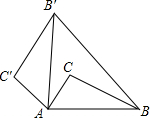 如图,将△ABC绕点A逆时针旋转80°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )
如图,将△ABC绕点A逆时针旋转80°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )| A. | 82° | B. | 80° | C. | 78° | D. | 76° |
分析 先利用旋转的性质得到AB=AB′,∠AB′C′=∠ABC,∠BAB′=80°,则根据等腰三角形的性质和三角形内角和定理计算出∠ABB′=∠AB′B=50°,于是可得到∠ABC=∠ABB′-∠B′BC=30°,所以∠AB′C′=30°,然后计算∠AB′B+∠AB′C′即可.
解答 解:∵△ABC绕点A逆时针旋转80°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),
∴AB=AB′,∠AB′C′=∠ABC,∠BAB′=80°,
∴∠ABB′=∠AB′B,
∴∠ABB′=∠AB′B=$\frac{1}{2}$(180°-80°)=50°,
∵∠ABC=∠ABB′-∠B′BC=80°-50°=30°,
∴∠AB′C′=30°,
∴∠BB′C′=∠AB′B+∠AB′C′=50°+30°=80°.
故选B.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.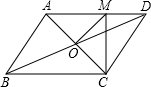 如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,如果△CDM的周长是40cm,则平行四边形ABCD的周长是( )
如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,如果△CDM的周长是40cm,则平行四边形ABCD的周长是( )
 如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,如果△CDM的周长是40cm,则平行四边形ABCD的周长是( )
如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,如果△CDM的周长是40cm,则平行四边形ABCD的周长是( )| A. | 40cm | B. | 60cm | C. | 70cm | D. | 80cm |
14.甲、乙两人各有两张扑克牌,甲的牌点数是3,5,乙的牌点数是4,6,如果两人各自从自己牌中任取一张,记事件“甲的点数大于乙的点数”为事件A;如果将两人的牌放在一起洗匀,记事件“两人同时各取一张,点数和为偶数”为事件B,则P(A)+P(B)的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{7}{12}$ | C. | $\frac{3}{4}$ | D. | 1 |
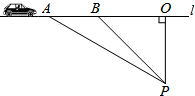 超速行驶容易引发交通事故.如图,某观测点设在到公路l的距离为100米的点P处,一辆汽车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,是判断此车是否超过了每小时80千米的限制速度?
超速行驶容易引发交通事故.如图,某观测点设在到公路l的距离为100米的点P处,一辆汽车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,是判断此车是否超过了每小时80千米的限制速度?
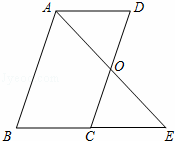 已知:?ABCD中,E是CD的中点,AE的延长线与BC的延长线相交于点F.求证:BC=CF.
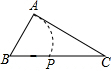
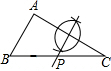
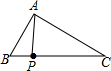
已知:?ABCD中,E是CD的中点,AE的延长线与BC的延长线相交于点F.求证:BC=CF. 如图,在钝角△ABC中,AC<BC,用尺规在BC上确定一点P,使PA+PC=BC,下面是四个同学的作法(只留下了作图痕迹,未连接PA),其中正确的是( )
如图,在钝角△ABC中,AC<BC,用尺规在BC上确定一点P,使PA+PC=BC,下面是四个同学的作法(只留下了作图痕迹,未连接PA),其中正确的是( )