题目内容
12.计算与化简:(1)$\sqrt{25}$-$\sqrt{\frac{1}{18}}$+$\frac{1}{\sqrt{2}-1}$
(2)$\sqrt{3{a}^{2}}$÷3$\sqrt{\frac{a}{2}}$×$\frac{1}{2}$$\sqrt{\frac{2a}{3}}$
(3)$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$
(4)$\frac{{x}^{2}-4}{{x}^{2}+2x+1}$÷(x+2)•$\frac{x+1}{2-x}$.
分析 (1)先对原式化简,再合并同类项即可解答本题;
(2)根据二次根式乘除法的计算方法进行计算即可;
(3)先对原式化简,再合并同类项即可解答本题;
(4)根据分式的乘除法的计算方法进行计算即可解答本题.
解答 解:(1)$\sqrt{25}$-$\sqrt{\frac{1}{18}}$+$\frac{1}{\sqrt{2}-1}$
=$5-\frac{\sqrt{2}}{6}+\sqrt{2}+1$
=$6+\frac{5\sqrt{2}}{6}$;
(2)$\sqrt{3{a}^{2}}$÷3$\sqrt{\frac{a}{2}}$×$\frac{1}{2}$$\sqrt{\frac{2a}{3}}$
=$a\sqrt{3}×\frac{\sqrt{2}}{3\sqrt{a}}×\sqrt{\frac{a}{6}}$
=$\frac{a}{3}$;
(3)$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$
=$\sqrt{16}-\sqrt{6}+2\sqrt{6}$
=$4-\sqrt{6}+2\sqrt{6}$
=$4+\sqrt{6}$;
(4)$\frac{{x}^{2}-4}{{x}^{2}+2x+1}$÷(x+2)•$\frac{x+1}{2-x}$
=$\frac{(x+2)(x-2)}{(x+1)^{2}}×\frac{1}{x+2}×\frac{x+1}{2-x}$
=$-\frac{1}{x+1}$.
点评 本题考查二次根式的混合运算、分式的混合运算,解题的关键是明确它们各自的计算方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.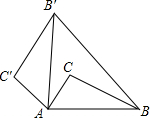 如图,将△ABC绕点A逆时针旋转80°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )
如图,将△ABC绕点A逆时针旋转80°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )
 如图,将△ABC绕点A逆时针旋转80°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )
如图,将△ABC绕点A逆时针旋转80°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )| A. | 82° | B. | 80° | C. | 78° | D. | 76° |
2. 如图,在数轴上表示数$\frac{\sqrt{5}}{5}$×(-5)的点可能是( )
如图,在数轴上表示数$\frac{\sqrt{5}}{5}$×(-5)的点可能是( )
 如图,在数轴上表示数$\frac{\sqrt{5}}{5}$×(-5)的点可能是( )
如图,在数轴上表示数$\frac{\sqrt{5}}{5}$×(-5)的点可能是( )| A. | 点E | B. | 点F | C. | 点P | D. | 点Q |
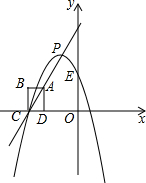 如图,在平面直角坐标系中,边长为1的正方形ABCD的顶点A在直线y=2x+4上,点B在第二象限,C,D两点均在x轴上,且点C在点D的左侧,抛物线y=-(x-m)2+n的顶点P在直线y=2x+4上运动,且这条抛物线交y轴于点E.
如图,在平面直角坐标系中,边长为1的正方形ABCD的顶点A在直线y=2x+4上,点B在第二象限,C,D两点均在x轴上,且点C在点D的左侧,抛物线y=-(x-m)2+n的顶点P在直线y=2x+4上运动,且这条抛物线交y轴于点E.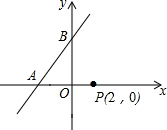 如图,在平面直角坐标系中,点P的坐标为(2,0),直线y=$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM的最小值为4.
如图,在平面直角坐标系中,点P的坐标为(2,0),直线y=$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM的最小值为4.