题目内容
17.在“全民读书月”活动中,某校九年级的小明调查了班级40名同学计划购买课外书的费用情况,并对调查结果进行整理,绘制了下面两个不完整的统计图.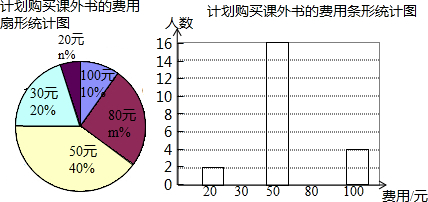
(1)直接补全条形统计图;
(2)m=25,n=5;
(3)在扇形统计图中,“30元”所在扇形的圆心角的度数是72°;
(4)如果该校九年级共有学生320人,那么请你估计计划购买课外书的费用为80元的九年级学生有多少?
分析 (1)总人数乘以30元所占百分比可得30元人数,用总人数减去其余各组人数可得80元的人数,补全条形图;
(2)用20元、80元的人数除以总人数可得其所占百分比;
(3)用360°乘以30元占总数的百分比;
(4)用总体中人数×样本中80元所占比例可得.
解答 解:(1)费用为30元的有:40×20%=8人,费用为80元的有:40-2-8-16-4=10人,
补全条形统计图如下: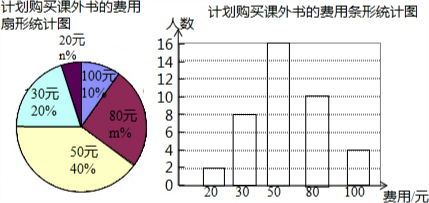
(2)m=$\frac{10}{40}×100$=25,n=$\frac{2}{40}$×100=5;
(3)360°×20%=72°;
(4)320×25%=80人.
答:估计计划购买课外书的费用为80元的九年级学生约有80人.
故答案为:(2)25,5;(3)72°.
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
8. 某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
请根据以上图表信息解答下列问题:
(1)频数分布表中的m=48,n=0.3;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为108°;
(3)从选择“篮球”选项的60名学生中,随机抽取10名学生作为代表进行投篮测试,则其中某位学生被选中的概率是$\frac{1}{6}$.
 某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:| 运动项目 | 频数(人数) | 频率 |
| 篮球 | 60 | 0.25 |
| 羽毛球 | m | 0.20 |
| 乒乓球 | 72 | n |
| 跳绳 | 36 | 0.15 |
| 其它 | 24 | 0.10 |
(1)频数分布表中的m=48,n=0.3;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为108°;
(3)从选择“篮球”选项的60名学生中,随机抽取10名学生作为代表进行投篮测试,则其中某位学生被选中的概率是$\frac{1}{6}$.
5.袋子中装有2个黑球和3个白球,这些球除了颜色不同外形状、大小、质地等完全相同,在看不到球的条件下,随机地一次从袋子中摸出三个球.下列事件是必然事件的是( )
| A. | 摸出的三个球中至少有一个球是白球 | |
| B. | 摸出的三个球中至少有一个球是黑球 | |
| C. | 摸出是三个球中至少有两个球的黑球 | |
| D. | 摸出的单个球中至少有两个球是白球 |
2.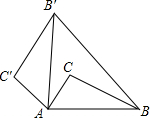 如图,将△ABC绕点A逆时针旋转80°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )
如图,将△ABC绕点A逆时针旋转80°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )
 如图,将△ABC绕点A逆时针旋转80°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )
如图,将△ABC绕点A逆时针旋转80°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接BB′,若∠B′BC=20°,则∠BB′C′的大小是( )| A. | 82° | B. | 80° | C. | 78° | D. | 76° |
9.下列运算正确的是( )
| A. | 3a3+4a3=7a6 | B. | 3a2•4a2=12a2 | C. | (a+2)2=a2+4 | D. | (a+b)(a-b)=a2-b2 |
6.从《陕西省页岩气地质调查与评价》获悉,我省页岩气资源储量约为4.44万亿立方米,把4.44万亿用科学记数法表示为( )
| A. | 4.44×108 | B. | 4.44×1010 | C. | 4.44×1011 | D. | 4.44×1012 |