题目内容
7．
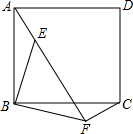如图，E为正方形ABCD内一点，△AEB按顺时针方向旋转一个角度后成为△CFB，则旋转了90度．
分析 首先根据旋转的定义，可得旋转中心为点B，然后判断出AB按顺时针方向旋转到BC所在的位置，旋转了90度，所以△AEB按顺时针方向旋转一个角度后成为△CFB，旋转了90度，据此解答即可．
解答 解：∵AB按顺时针方向旋转到BC所在的位置，旋转了90度，
∴△AEB按顺时针方向旋转一个角度后成为△CFB，则旋转了90度．
故答案为：90．
点评 此题主要考查了旋转的定义和性质的应用，要熟练掌握，解答此题的关键是判断出：（1）旋转中心为点B；（2）AB按顺时针方向旋转到BC所在的位置，旋转了90度．
练习册系列答案
相关题目
已知，一次函数y=-$\frac{3}{4}$x+6的图象与x轴交于A，与y轴交于C，以O，A，C为顶点在第一象限作矩形OABC．
18．
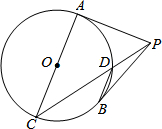如图，PA、PB是⊙O的切线，A、B是切点，AC是⊙O的直径，连PC交⊙O于点D，若BD∥AC，则tan∠ACP的值是（ ）
如图，PA、PB是⊙O的切线，A、B是切点，AC是⊙O的直径，连PC交⊙O于点D，若BD∥AC，则tan∠ACP的值是（ ）| A． | $\frac{3}{\sqrt{3}}$ | B． | $\sqrt{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{3\sqrt{3}}{5}$ |
已知：如图，AB是⊙O的直径，BC切⊙O于B，AC交⊙O于P，D为BC边的中点，连接DP．
如图，点P为双曲线y=$\frac{k}{x}$上一点，PE⊥x轴于点E，PF⊥y轴于点F，直线y=-$\frac{1}{2}$x+2与y轴、x轴分别交于点A、B，与PF、PE分别交于点C、D，若AD•BC=10，则k=4．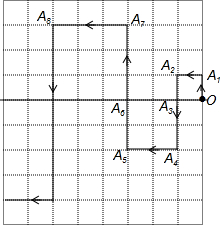
在平面直角坐标系中，一蚂蚁从原点O出发，按向上、向左、向下、向左的方向依次不断移动得A1，A2，A3，A4，A5，…，每次移动的距离分别为1，1，1，2，2，2，3，3，3…，其行走路线如图所示：
如图，将矩形纸片的两只直角分别沿EF、DF翻折，点B恰好落在AD边上的点B′处，点C恰好落在边B′F上．若AE=3，BE=5，则FC=4．
在?ABCD中，∠ABC，∠CDA的平分线分别交AD，CB的延长线于点E，F，求证：DE=BF．
17．等腰三角形的底边长10cm，周长36cm，则底角的余弦值为（ ）
| A． | $\frac{5}{12}$ | B． | $\frac{12}{5}$ | C． | $\frac{5}{13}$ | D． | $\frac{12}{13}$ |