题目内容
18.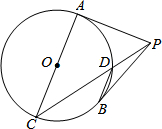 如图,PA、PB是⊙O的切线,A、B是切点,AC是⊙O的直径,连PC交⊙O于点D,若BD∥AC,则tan∠ACP的值是( )
如图,PA、PB是⊙O的切线,A、B是切点,AC是⊙O的直径,连PC交⊙O于点D,若BD∥AC,则tan∠ACP的值是( )| A. | $\frac{3}{\sqrt{3}}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{3\sqrt{3}}{5}$ |
分析 连接AD,CB,过点P作PE⊥CB交CB的延长线于E,由PA、PB是⊙O的切线,得到PA=PB,∠3=∠5,1=2,由于AC∥BD,得到∠ACB=∠DBE,推出∠3=4,∠5=4,通过△ADP≌△BPE,得到AD=BE,PD=PE,设PE=PD=a,BE=BC=AD=b,由射影定理得$\frac{a}{b}$=$\frac{\sqrt{2}}{2}$,于是得到结果tan∠ACP=$\frac{AD}{CD}$=$\frac{\sqrt{2}}{2}$.
解答 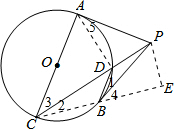 解:连接AD,CB,过点P作PE⊥CB交CB的延长线于E,如图,
解:连接AD,CB,过点P作PE⊥CB交CB的延长线于E,如图,
∵PA、PB是⊙O的切线,
∴PA=PB,∠3=∠5,1=2,
∵AC∥BD,
∴∠ACB=∠DBE,
∴∠3=4,
∴∠5=4,
在△ADP与△BEP中,$\left\{\begin{array}{l}{∠ADP=PEB=90°}\\{∠5=∠4}\\{PA=PB}\end{array}\right.$,
∴△ADP≌△BPE,
∴AD=BE,PD=PE,
∵AC∥BD,
∴AD=BC,
设PE=PD=a,BE=BC=AD=b,
∵∠CAP=90°,
由射影定理得:AD2=PD•CD,
∴CD=$\frac{{AD}^{2}}{PD}$=$\frac{{b}^{2}}{a}$,
∴PC=$\frac{{b}^{2}}{a}$+a,CE=2b,
在Rt△PCE中,(2b)2+a2=${(\frac{{b}^{2}}{a}+a)}^{2}$,
∴$\frac{a}{b}$=$\frac{\sqrt{2}}{2}$,
∴tan∠ACP=$\frac{AD}{CD}$=$\frac{\sqrt{2}}{2}$,
故选C.
点评 本题考查了切线性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

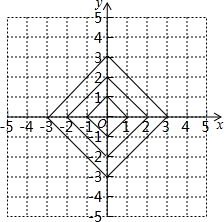 在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,观察如图所示中每一个正方形(实践)四条边上的整点的个数,请你猜测由里向外第7个正方形(实线)四条边上的整点个数有( )
在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,观察如图所示中每一个正方形(实践)四条边上的整点的个数,请你猜测由里向外第7个正方形(实线)四条边上的整点个数有( )| A. | 24个 | B. | 28个 | C. | 32个 | D. | 30个 |
| A. | x≥-2 | B. | x>-2 | C. | x<-2 | D. | x≤-2 |
 ”标志所在的正方形是正方体中的( )
”标志所在的正方形是正方体中的( )
| A. | 面CDHE | B. | 面BCEF | C. | 面ABFG | D. | 面ADHG |
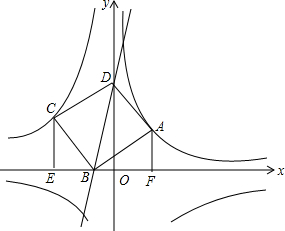 如图,点A(2,2)在双曲线y1=$\frac{k}{x}$(x>0)上,点C在双曲线y2=-$\frac{9}{x}$(x<0)上,分别过A、C向x轴作垂线,垂足分别为F、E,以A、C为顶点作正方形ABCD,且使点B在x轴上,点D在y轴的正半轴上.
如图,点A(2,2)在双曲线y1=$\frac{k}{x}$(x>0)上,点C在双曲线y2=-$\frac{9}{x}$(x<0)上,分别过A、C向x轴作垂线,垂足分别为F、E,以A、C为顶点作正方形ABCD,且使点B在x轴上,点D在y轴的正半轴上.
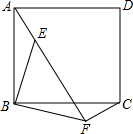 如图,E为正方形ABCD内一点,△AEB按顺时针方向旋转一个角度后成为△CFB,则旋转了90度.
如图,E为正方形ABCD内一点,△AEB按顺时针方向旋转一个角度后成为△CFB,则旋转了90度.