题目内容
12.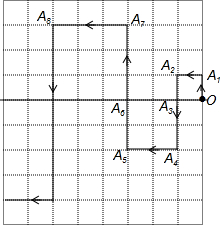 在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向左、向下、向左的方向依次不断移动得A1,A2,A3,A4,A5,…,每次移动的距离分别为1,1,1,2,2,2,3,3,3…,其行走路线如图所示:
在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向左、向下、向左的方向依次不断移动得A1,A2,A3,A4,A5,…,每次移动的距离分别为1,1,1,2,2,2,3,3,3…,其行走路线如图所示:(1)填写下列各点的坐标:A3(-1,0)、A6(-3,0)、A9(-6,0);
(2)写出点A3n的坐标(n为正整数);
(3)蚂蚁从原点O到点A33移动的距离是66.
分析 根据图象可得移动3次图象完成一个循环,从而可得出点的坐标,进而得出规律解答即可.
解答 解:(1)A3(-1,0)、A6(-3,0)、A9(-6,0),A12(-10,0);
(2)由(1)得出规律为:点A3n的坐标为(-$\frac{1}{2}$n(n+1),0).
(3)蚂蚁从原点O到点A33移动的距离是$\frac{1}{2}$×11×12=66.
故答案为:A3(-1,0)、A6(-3,0)、A9(-6,0);66.
点评 本题考查了点的规律变化,解答本题的关键是仔细观察图象,得到点的变化规律,难度一般.

练习册系列答案
相关题目
3.不等式3x>-6的解集为( )
| A. | x≥-2 | B. | x>-2 | C. | x<-2 | D. | x≤-2 |
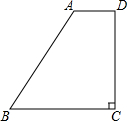 如图,有一块梯形空地ABCD可供停车,AD∥BC,∠C=90°,∠B=53°,AD=1.6m,CD=5.2m,现有一辆长4.9m,宽1.9m的汽车需要完全停入梯形区域,请你设计一种停车方案,并通过计算说明理由.(参考数据:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$)
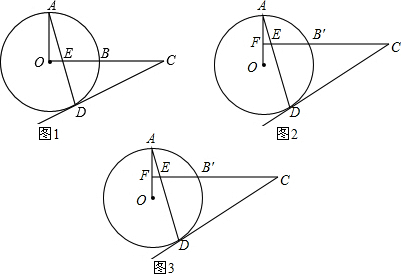
如图,有一块梯形空地ABCD可供停车,AD∥BC,∠C=90°,∠B=53°,AD=1.6m,CD=5.2m,现有一辆长4.9m,宽1.9m的汽车需要完全停入梯形区域,请你设计一种停车方案,并通过计算说明理由.(参考数据:sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$)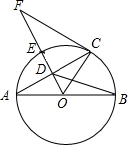 如图,AB是⊙O的直径,OD垂直弦AC于点D,OD的延长线交⊙O 于点E,与过点C的⊙O的切线交于点F,已知OD=3,DE=2.
如图,AB是⊙O的直径,OD垂直弦AC于点D,OD的延长线交⊙O 于点E,与过点C的⊙O的切线交于点F,已知OD=3,DE=2.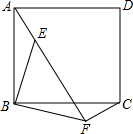 如图,E为正方形ABCD内一点,△AEB按顺时针方向旋转一个角度后成为△CFB,则旋转了90度.
如图,E为正方形ABCD内一点,△AEB按顺时针方向旋转一个角度后成为△CFB,则旋转了90度. 如图,在平面直角坐标系中,正方形OBCD的点B的坐标为(2,0),E,F分别为边BC,CD上的点,且BE=CF,连结OE,BF,交点为G,将△BCF沿BF对折,得到△BPF,延长FP交x轴于点Q.
如图,在平面直角坐标系中,正方形OBCD的点B的坐标为(2,0),E,F分别为边BC,CD上的点,且BE=CF,连结OE,BF,交点为G,将△BCF沿BF对折,得到△BPF,延长FP交x轴于点Q. 如图,⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBF,过点A作AD⊥BF,垂足为D.
如图,⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBF,过点A作AD⊥BF,垂足为D.