题目内容
2. 如图,点P为双曲线y=$\frac{k}{x}$上一点,PE⊥x轴于点E,PF⊥y轴于点F,直线y=-$\frac{1}{2}$x+2与y轴、x轴分别交于点A、B,与PF、PE分别交于点C、D,若AD•BC=10,则k=4.
如图,点P为双曲线y=$\frac{k}{x}$上一点,PE⊥x轴于点E,PF⊥y轴于点F,直线y=-$\frac{1}{2}$x+2与y轴、x轴分别交于点A、B,与PF、PE分别交于点C、D,若AD•BC=10,则k=4.
分析 先设P点的坐标为(a,$\frac{k}{a}$),则把y=$\frac{k}{a}$代入直线y=-$\frac{1}{2}$x+2即可求出C点的纵坐标,同理求出D点坐标,再根据直线y=-$\frac{1}{2}$x+2的解析式求出出A、B两点的坐标,再根据两点间的距离公式列出AD•BC=10,得到关于k的方程,解方程即可.
解答 解:设P点的坐标为(a,$\frac{k}{a}$),则D(a,-$\frac{1}{2}$a+2)、C(4-$\frac{2k}{a}$,$\frac{k}{a}$),
∵直线y=-x+2分别与x轴、y轴交于点A、B,
∴A(0,2)、B(4,0),
∵AD•BC=$\sqrt{(a-0)^{2}+(-\frac{1}{2}a+2-2)^{2}}$•$\sqrt{(4-\frac{2k}{a}-4)^{2}+(\frac{k}{a}-0)^{2}}$=10,
整理得,$\frac{5k}{2}$=10,
解得k=4.
故答案为4.
点评 本题考查的是一次函数及反比例函数的性质,先设出P点坐标,再表示出C、D两点的坐标是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
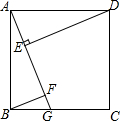 已知:在正方形ABCD中,点G是BC边上的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.求证:AF=BF+EF.
已知:在正方形ABCD中,点G是BC边上的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.求证:AF=BF+EF.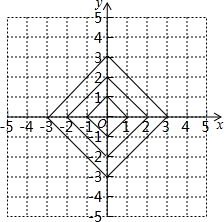 在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,观察如图所示中每一个正方形(实践)四条边上的整点的个数,请你猜测由里向外第7个正方形(实线)四条边上的整点个数有( )
在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,观察如图所示中每一个正方形(实践)四条边上的整点的个数,请你猜测由里向外第7个正方形(实线)四条边上的整点个数有( )
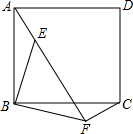 如图,E为正方形ABCD内一点,△AEB按顺时针方向旋转一个角度后成为△CFB,则旋转了90度.
如图,E为正方形ABCD内一点,△AEB按顺时针方向旋转一个角度后成为△CFB,则旋转了90度.
 如图,AB是⊙O的直径,弦CD和AB相交于P,且∠APC=45°,OQ是弦CD的弦心距.
如图,AB是⊙O的直径,弦CD和AB相交于P,且∠APC=45°,OQ是弦CD的弦心距.