题目内容
16.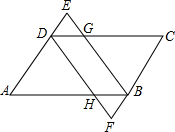 在?ABCD中,∠ABC,∠CDA的平分线分别交AD,CB的延长线于点E,F,求证:DE=BF.
在?ABCD中,∠ABC,∠CDA的平分线分别交AD,CB的延长线于点E,F,求证:DE=BF.
分析 利用平行四边形的性质得出结合角平分线的性质和平行线的性质得出∠AHD=∠ABG,进而得出四边形DFBE是平行四边形,即可得出答案.
解答 证明:∵在?ABCD中,∠ABC,∠CDA的平分线分别交AD,CB的延长线于点E,F,
∴AE∥CF,DC∥AB,∠ADC=∠ABC,则∠ADH=∠CDH=∠CBG=∠ABG,
∴∠CDH=∠DHA,
∴∠AHD=∠ABG,
∴DH∥BG,
∴四边形DFBE是平行四边形,
∴DE=BF.
点评 此题主要考查了平行四边形的判定与性质,得出四边形DFBE是平行四边形是解题关键.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
8.将图1围成图2的正方体,则图1中的红心“ ”标志所在的正方形是正方体中的( )
”标志所在的正方形是正方体中的( )

 ”标志所在的正方形是正方体中的( )
”标志所在的正方形是正方体中的( )
| A. | 面CDHE | B. | 面BCEF | C. | 面ABFG | D. | 面ADHG |
5.关于x的一元二次方程x2-3x+m=0有两个不相等的实数根,则实数m的取值范围为( )
| A. | m≥$\frac{9}{4}$ | B. | m<$\frac{9}{4}$ | C. | m=$\frac{9}{4}$ | D. | m<-$\frac{9}{4}$ |

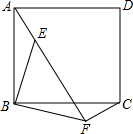 如图,E为正方形ABCD内一点,△AEB按顺时针方向旋转一个角度后成为△CFB,则旋转了90度.
如图,E为正方形ABCD内一点,△AEB按顺时针方向旋转一个角度后成为△CFB,则旋转了90度. 如图,在平面直角坐标系中,正方形OBCD的点B的坐标为(2,0),E,F分别为边BC,CD上的点,且BE=CF,连结OE,BF,交点为G,将△BCF沿BF对折,得到△BPF,延长FP交x轴于点Q.
如图,在平面直角坐标系中,正方形OBCD的点B的坐标为(2,0),E,F分别为边BC,CD上的点,且BE=CF,连结OE,BF,交点为G,将△BCF沿BF对折,得到△BPF,延长FP交x轴于点Q. 如图,AB是⊙O的直径,弦CD和AB相交于P,且∠APC=45°,OQ是弦CD的弦心距.
如图,AB是⊙O的直径,弦CD和AB相交于P,且∠APC=45°,OQ是弦CD的弦心距. 如图,⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBF,过点A作AD⊥BF,垂足为D.
如图,⊙O为△ABC的外接圆,BC为⊙O的直径,BA平分∠CBF,过点A作AD⊥BF,垂足为D. 如图,AM是△ABC的中线.
如图,AM是△ABC的中线.