题目内容
1. 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.
在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.
分析 过C点作CD⊥AB于点D.先在Rt△CDA中求得AD、CD的长,再利用勾股定理求得BD的长,AB=BD-AD,即可得出结果.
解答 解:过点C作CD⊥AB于D,如图所示: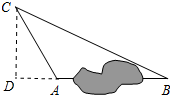
在Rt△CDA中∠CAD=180°-∠CAB=180°-120°=60°,
∵sin∠CAD=$\frac{CD}{AC}$,
∴CD=AC•sin60°=50×$\frac{\sqrt{3}}{2}$=25$\sqrt{3}$(m),
同理:AD=AC•cos60°=50×$\frac{1}{2}$=25(m),
在Rt△CBD中,$BD=\sqrt{B{C^2}-C{D^2}}=\sqrt{{{100}^2}-{{(25\sqrt{3})}^2}}=25\sqrt{13}$(m),
∴AB=BD-AD=$25\sqrt{13}-25$(m),
答:AB之间的距离是($25\sqrt{13}-25$)m.
点评 本题考查了解直角三角形的应用、三角函数、勾股定理;解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
9.(1)一个不透明的盒中装有若干个除颜色外都相同的红球与黄球.在这个口袋中先放入2个白球,再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色后放回盒中,再继续摸球,全班一共做了400次这样的摸球试验.如果知道摸出白球的频数是40,你能估计在未放入白球前,袋中原来共有多少个小球吗?
(2)提出问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
活动操作:先从盒中摸出8个球,画上记号放回盒中.再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色、是否有记号,放回盒中,再继续摸球、记录、放回袋中.
统计结果:摸球试验活动一共做了50次,统计结果如下表:
由上述的摸球试验推算:
①盒中红球、黄球各占总球数的百分比分别是多少?
②盒中有红球多少个?
(2)提出问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
活动操作:先从盒中摸出8个球,画上记号放回盒中.再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色、是否有记号,放回盒中,再继续摸球、记录、放回袋中.
统计结果:摸球试验活动一共做了50次,统计结果如下表:
| 球的类别 | 无记号 | 有记号 | ||
| 红色 | 黄色 | 红色 | 黄色 | |
| 摸到的次数 | 18 | 28 | 2 | 2 |
①盒中红球、黄球各占总球数的百分比分别是多少?
②盒中有红球多少个?
13.下列图形不是轴对称图形的是( )
| A. | 正方形 | B. | 等腰三角形 | C. | 圆 | D. | 平行四边形 |
10.一元二次方程x2+8x-9=0配方后得到的方程是( )
| A. | (x-4)2+7=0 | B. | (x+4)2=25 | C. | (x-4)2=25 | D. | (x+4)2-7=0 |
11.如果a>b,那么下列不等式不成立的是( )
| A. | a-5>b-5 | B. | -5a>-5b | C. | $\frac{a}{2}$>$\frac{b}{2}$ | D. | -0.5a<-0.5b |
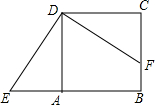 如图,正方形ABCD中,点F在边BC上,E在边BA的延长线上,△DCF按顺时针方向旋转后恰好与△DAE重合,若AE=3,BF=2,则四边形BFDE的面积是25.
如图,正方形ABCD中,点F在边BC上,E在边BA的延长线上,△DCF按顺时针方向旋转后恰好与△DAE重合,若AE=3,BF=2,则四边形BFDE的面积是25.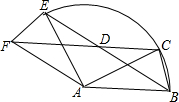 如图,△ABC中,AB=AC=2,∠BAC=30°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D,$\widehat{BE}$是点B旋转形成的弧.
如图,△ABC中,AB=AC=2,∠BAC=30°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D,$\widehat{BE}$是点B旋转形成的弧.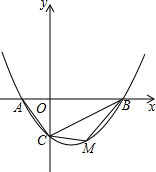 如图,抛物线y=ax2-$\frac{3}{2}$x-2(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,已知B点坐标为(4,0).
如图,抛物线y=ax2-$\frac{3}{2}$x-2(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,已知B点坐标为(4,0). 如图,三个小正方形的边长都为3,则图中阴影部分面积的和是$\frac{27}{8}$π.(结果保留π)
如图,三个小正方形的边长都为3,则图中阴影部分面积的和是$\frac{27}{8}$π.(结果保留π)