题目内容
16.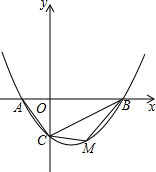 如图,抛物线y=ax2-$\frac{3}{2}$x-2(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,已知B点坐标为(4,0).
如图,抛物线y=ax2-$\frac{3}{2}$x-2(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,已知B点坐标为(4,0).(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在一点P,使得PB+PC的和最小?若存在,求出P点坐标;若不存在,请说明理由;
(3)若点M是线段BC下方的抛物线上一点,求△MBC面积的最大值,并求出此时M点的坐标.
分析 (1)将点B的坐标代入代入抛物线的解析式,可求得a的值,将a的值代入可求得抛物线的解析式;
(2)先求得点C的坐标,然后依据待定系数法求得直线BC的解析式,然后再求得抛物线的对称轴方程,由三角形的三边关系可知当点P、C、B在一条直线上时,PC+PB有最小值,最后将点P的横坐标代入直线BC的解析式可求得点P的纵坐标;
(3)过点M作MD⊥x轴,交直线BC与点D.设点M(a,$\frac{1}{2}{a}^{2}-\frac{3}{2}a-2$),则点D(a,$\frac{1}{2}a-2$).于是可求得DM的长(用含a的式子表示),接下来,依据三角形的面积公式得到△CMB的面积与a的函数关系式,最后依据配方法可求得△CMB的面积的最大值以及点a的值.
解答 解:(1)∵将点B的坐标代入得:16a-6-2=0,解得:a=$\frac{1}{2}$,
∴抛物线的解析式为y=$\frac{1}{2}{x}^{2}-\frac{3}{2}x-2$.
(2)如图1所示:
∵PC+PB≥BC,
∴当点P、C、B在一条直线上时,PC+PB有最小值.
∵令x=0得;y=-2,
∴点C的坐标为(0,-2).
设直线BC的解析式为y=kx+b.
∵将点B、C的坐标代入得:$\left\{\begin{array}{l}{4k+b=0}\\{b=-2}\end{array}\right.$,解得:k=$\frac{1}{2}$,b=-2,
∴直线BC的解析式为y=$\frac{1}{2}x$-2.
∵抛物线的对称轴为x=-$\frac{b}{2a}$=$\frac{\frac{3}{2}}{2×\frac{1}{2}}$=$\frac{3}{2}$,
∴点P的横坐标为$\frac{3}{2}$.
∵将x=$\frac{3}{2}$代入直线BC的解析式得;y=$\frac{1}{2}×\frac{3}{2}$-2=-$\frac{5}{4}$,
∴点P的坐标为($\frac{3}{2}$,-$\frac{5}{4}$).
(3)过点M作MD⊥x轴,交直线BC与点D.
设点M(a,$\frac{1}{2}{a}^{2}-\frac{3}{2}a-2$),则点D(a,$\frac{1}{2}a-2$).DM=$\frac{1}{2}a-2$-($\frac{1}{2}{a}^{2}-\frac{3}{2}a-2$)=-$\frac{1}{2}$a2+2a.
∵△CMB的面积=$\frac{1}{2}$MD•OB=$\frac{1}{2}$×4×(-$\frac{1}{2}$a2+2a)=-a2+4a=-(a-2)2+4,
∴当a=2时,△CMB的面积有最大值,△CMB的最大面积=4.
∴点M(2,-3).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数、一次函数的解析式、三角形的面积公式、配方法求二次函数的最值,列出△CMB的面积与a的函数关系式是解题的关键.

| A. | -|-2| | B. | (-2)0 | C. | -(-2) | D. | (-2)-1 |
| A. | $-\frac{2}{3}$ | B. | $-\frac{3}{2}$ | C. | $-\frac{9}{4}$ | D. | $-\frac{4}{9}$ |
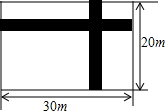 如图,在宽为20米,长为30米的矩形地面上修建两条同样宽为x米的道路,余下部分作为耕地,则耕地面积表示为( )
如图,在宽为20米,长为30米的矩形地面上修建两条同样宽为x米的道路,余下部分作为耕地,则耕地面积表示为( )| A. | (30-x)(20-x)-x2 | B. | (30-x)(20-x) | C. | (30-2x)(20-2x) | D. | (30-2x)(20-x) |
| A. | x≠2 | B. | x>2 | C. | x<2 | D. | x≥2 |
 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.
在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.