题目内容
已知二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)经过A、B、C、D四个点,其中横坐标x与纵坐标y的对应值如表:
(1)求二次函数解析式;
(2)求△ABD的面积.
| A | B | C | D | |
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
(2)求△ABD的面积.
考点:待定系数法求二次函数解析式,二次函数的性质
专题:
分析:(1)把点A,B,C的坐标代入y=ax2+bx+c,即可求出二次函数解析式,
(2)利用三角形的面积公式求解即可.
(2)利用三角形的面积公式求解即可.
解答:解:(1)把点A,B,C的坐标代入y=ax2+bx+c,得
,解得
,
所以二次函数解析式y=-x2+3x+3;
(2)S△ABD=
×3×4=6.
|
|
所以二次函数解析式y=-x2+3x+3;
(2)S△ABD=
| 1 |
| 2 |
点评:本题主要考查了用待定系数法求二次函数的解析式及二次函数的性质,解题的关键是正确的求出二次函数解析式.

练习册系列答案
相关题目
⊙O的半径为5cm,弦AB∥CD,且AB=8cm,CD=6cm,则AB与CD之间的距离为( )
| A、1cm |
| B、7cm |
| C、3cm或4cm |
| D、1cm或7cm |
一个圆锥模型,它的底面半径为1,高为2
,则这个圆锥的侧面积是( )
| 2 |
| A、4π | ||
| B、3π | ||
C、2
| ||
| D、2π |
 ⊙O中,OD⊥AB于C,AE过点O,连接EC,若AB=8,CD=2,则EC长度为( )
⊙O中,OD⊥AB于C,AE过点O,连接EC,若AB=8,CD=2,则EC长度为( )A、2
| ||
| B、8 | ||
C、2
| ||
D、2
|
 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
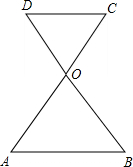 如图,AC与BD相交于点O,若OA=OB,∠A=60°,且AB∥CD,求证:△OCD是等边三角形.
如图,AC与BD相交于点O,若OA=OB,∠A=60°,且AB∥CD,求证:△OCD是等边三角形.