题目内容
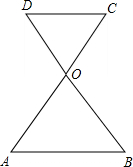 如图,AC与BD相交于点O,若OA=OB,∠A=60°,且AB∥CD,求证:△OCD是等边三角形.
如图,AC与BD相交于点O,若OA=OB,∠A=60°,且AB∥CD,求证:△OCD是等边三角形.考点:等边三角形的判定
专题:证明题
分析:根据OA=OB,得∠A=∠B=60°;根据AB∥DC,得出对应角相等,从而求得∠C=∠D=60°,根据等边三角形的判定就可证得结论.
解答:证明:∵OA=OB,
∴∠A=∠B=60°,
又∵AB∥DC,
∴∠A=∠C=60°,∠B=∠D=60°,
∴△OCD是等边三角形.
∴∠A=∠B=60°,
又∵AB∥DC,
∴∠A=∠C=60°,∠B=∠D=60°,
∴△OCD是等边三角形.
点评:本题主要考查了等边三角形的判定和平行线的性质:两直线平行,内错角相等.

练习册系列答案
相关题目
将抛物线y=(x-1)2向左平移2个单位,所得抛物线的表达式为( )
| A、y=(x+1)2 |
| B、y=(x-3)2 |
| C、y=(x-1)2+2 |
| D、y=(x-1)2-2 |
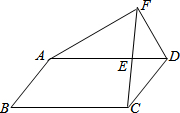 如图,已知点E在平行四边形ABCD的边AD上,AE=3ED,延长CE到点F,使得EF=CE,设
如图,已知点E在平行四边形ABCD的边AD上,AE=3ED,延长CE到点F,使得EF=CE,设 如图,若l1∥l2∥l3,如果DE=6,EF=2,BC=1.5,那么AC=
如图,若l1∥l2∥l3,如果DE=6,EF=2,BC=1.5,那么AC=