题目内容
⊙O的半径为5cm,弦AB∥CD,且AB=8cm,CD=6cm,则AB与CD之间的距离为( )
| A、1cm |
| B、7cm |
| C、3cm或4cm |
| D、1cm或7cm |
考点:垂径定理,勾股定理
专题:分类讨论
分析:先根据题意画出图形,注意圆心与两弦的位置关系有两种情况:同旁或两旁,画出图形,求出OE和OF,即可得出答案.
解答:解:过点O作OE⊥CD于E,
∵AB∥CD,
∴OF⊥AB
∵OE过圆心,OE⊥CD,
∴ED=
CD=3cm,
∵OD=5cm,
∴EO=4cm,
同理,OF=3cm,
∴EF=1cm,
当AB、CD位于圆心两旁时EF=7cm,
故选D.

∵AB∥CD,
∴OF⊥AB
∵OE过圆心,OE⊥CD,
∴ED=
| 1 |
| 2 |
∵OD=5cm,
∴EO=4cm,
同理,OF=3cm,
∴EF=1cm,
当AB、CD位于圆心两旁时EF=7cm,
故选D.
点评:本题考查了垂径定理和勾股定理的应用,解此题的关键是构造直角三角形,注意要进行分类讨论啊.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 如图,AB⊥b,DC⊥b,CA⊥a,ED⊥a.则图中能表示点到直线的距离的线段长的条数有( )
如图,AB⊥b,DC⊥b,CA⊥a,ED⊥a.则图中能表示点到直线的距离的线段长的条数有( )| A、4 | B、7 | C、8 | D、12 |
抛物线y=(m-1)x2-mx-m2+1的图象过原点,则m的值为( )
| A、±1 | B、0 | C、1 | D、-1 |
在下列y关于x的函数中,一定是二次函数的是( )
| A、y=x2 | ||
B、y=
| ||
| C、y=kx2 | ||
| D、y=k2x |
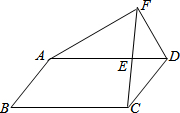 如图,已知点E在平行四边形ABCD的边AD上,AE=3ED,延长CE到点F,使得EF=CE,设
如图,已知点E在平行四边形ABCD的边AD上,AE=3ED,延长CE到点F,使得EF=CE,设 如图,若l1∥l2∥l3,如果DE=6,EF=2,BC=1.5,那么AC=
如图,若l1∥l2∥l3,如果DE=6,EF=2,BC=1.5,那么AC=