题目内容
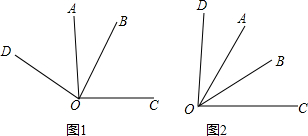
已知∠AOC=∠BOD=α(0°<α<180°)
(1)如图1,若α=90°
①写出图中一组相等的角(除直角外) ,理由是
②试猜想∠COD和∠AOB在数量上是相等、互余、还是互补的关系,并说明理由;
(2)如图2,∠COD+∠AOB和∠AOC满足的等量关系是 ;当α= °,∠COD和∠AOB互余.
(1)如图1,若α=90°
①写出图中一组相等的角(除直角外)
②试猜想∠COD和∠AOB在数量上是相等、互余、还是互补的关系,并说明理由;
(2)如图2,∠COD+∠AOB和∠AOC满足的等量关系是

考点:余角和补角
专题:
分析:(1)①根据同角的余角相等解答;
②表示出∠AOD,再求出∠COD,然后整理即可得解;
(2)根据(1)的求解思路解答即可.
②表示出∠AOD,再求出∠COD,然后整理即可得解;
(2)根据(1)的求解思路解答即可.
解答:解:(1)①∵∠AOC=∠BOD=90°,
∴∠AOD+∠AOB=∠BOC+∠AOB=90°,
∴∠AOD=∠BOC;
②∵∠AOD=∠BOD-∠AOB=90°-∠AOB,
∴∠COD=∠AOD+∠AOC=90°-∠AOB+90°,
∴∠AOB+∠COD=180°,
∴∠COD和∠AOB互补;
(2)由(1)可知∠COD+∠AOB=∠BOD+∠AOC=α+α=2α,
所以,∠COD+∠AOB=2∠AOC,
若∠COD和∠AOB互余,则2∠AOC=90°,
所以,∠AOC=45°,
即α=45°.
故答案为:(1)AOD=∠BOC,同角的余角相等;(2)互补,45.
∴∠AOD+∠AOB=∠BOC+∠AOB=90°,
∴∠AOD=∠BOC;
②∵∠AOD=∠BOD-∠AOB=90°-∠AOB,
∴∠COD=∠AOD+∠AOC=90°-∠AOB+90°,
∴∠AOB+∠COD=180°,
∴∠COD和∠AOB互补;
(2)由(1)可知∠COD+∠AOB=∠BOD+∠AOC=α+α=2α,
所以,∠COD+∠AOB=2∠AOC,
若∠COD和∠AOB互余,则2∠AOC=90°,
所以,∠AOC=45°,
即α=45°.
故答案为:(1)AOD=∠BOC,同角的余角相等;(2)互补,45.
点评:本题考查了余角和补角,熟记概念并准确识图,理清图中各角度之间的关系是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在下列y关于x的函数中,一定是二次函数的是( )
| A、y=x2 | ||
B、y=
| ||
| C、y=kx2 | ||
| D、y=k2x |
若x2+2pxy+4y2是完全平方式,则p等于( )
| A、1 | B、±2 | C、±4 | D、±1 |
在“感恩一日捐”捐赠活动中,某班40位同学捐款金额统计如下,
则在这次活动中,该班同学捐款金额的中位数是( )
| 金额(元/人) | 20 | 30 | 40 | 50 | 100 |
| 学生数(人) | 3 | 17 | 5 | 12 | 3 |
| A、30 元 | B、40元 |
| C、35元 | D、45元 |