题目内容
14.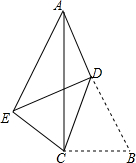 如图,在△ABC中,∠ACB=90°,BC=4,AB=10,点D是AB上的一点,将△DBC沿着CD折叠,此时点B与点E重合,连接AE,当D为AB的中点时,AE=$\frac{34}{5}$.
如图,在△ABC中,∠ACB=90°,BC=4,AB=10,点D是AB上的一点,将△DBC沿着CD折叠,此时点B与点E重合,连接AE,当D为AB的中点时,AE=$\frac{34}{5}$.
分析 连接EB交CD于点F,根据△BCD的面积等于△ABC的面积的一半求得△BCD的面积,根据面积公式求得BF的长,再在直角△BDF中,利用勾股定理求得DF的长,根据DF是△ABE的中位线即可求得.
解答 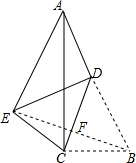 解:连接EB交CD于点F.
解:连接EB交CD于点F.
∵B和E关于CD对称,
∴BE⊥CD,且BF=EF.
在直角△ABC中,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{1{0}^{2}-{4}^{2}}$=2$\sqrt{21}$,CD=$\frac{1}{2}$AB=$\frac{1}{2}$×10=5.
S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×2$\sqrt{21}$×4=4$\sqrt{21}$,
∵D是AB的中点,
∴S△BCD=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×4$\sqrt{21}$=2$\sqrt{21}$.
∴$\frac{1}{2}$CD•BF=2$\sqrt{21}$,
解得:BF=$\frac{4\sqrt{21}}{5}$.
∴在直角△BDF中,DF=$\sqrt{B{D}^{2}-B{F}^{2}}$=$\sqrt{{5}^{2}-(\frac{4\sqrt{21}}{5})^{2}}$=$\frac{17}{5}$.
∵BF=EF,AD=BD,
∴AE=2DF=2×$\frac{17}{5}$=$\frac{34}{5}$.
故答案为:$\frac{34}{5}$.
点评 此题主要考查了解直角三角形以及勾股定理和翻折变换的性质,根据已知得出BF的长,进而利用勾股定理得出是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.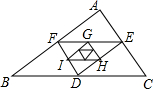 如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )
如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )
 如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )
如图,△DEF的顶点分别是△ABC各边的中点,△GHI的顶点分别是△DEF各边的中点,…,依次做下去,记△ABC得周长为P1,△DEF的周长为P2,△GHI的周长为P3,…,已知P1=1,则Pn等于( )| A. | $\frac{1}{{2}^{n-1}}$ | B. | $\frac{1}{{2}^{n}}$ | C. | $\frac{1}{{2}^{n+1}}$ | D. | $\frac{1}{{2}^{n+2}}$ |
4.要使分式$\frac{{x}^{2}+1}{{x}^{2}-1}$有意义,x满足的条件为( )
| A. | x≠0 | B. | x≠1 | C. | x≠1或x≠-1 | D. | x≠1且x≠-1 |