题目内容
3.已知m+n=2,mn=-2,则(1-m)(1-n)的值为( )| A. | -1 | B. | 1 | C. | -3 | D. | 5 |
分析 根据多项式乘以多项式的法则,可表示为(a+b)(m+n)=am+an+bm+bn,再代入计算即可.
解答 解:∵m+n=2,mn=-2,
∴(1-m)(1-n)=1-n-m+mn=1-(n+m)+mn=1-2-2=-3;
故选:C.
点评 本题主要考查多项式乘以多项式,掌握多项式乘以多项式的法则是本题的关键.注意不要漏项,漏字母,有同类项的合并同类项.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
8.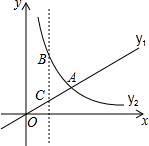 已知直线OA的解析式为y1=kx,且这条直线与x轴的正半轴的夹角为30°,y2=$\frac{\sqrt{3}}{x}$(x>0)的图象如图所示,则下列结论正确的是( )
已知直线OA的解析式为y1=kx,且这条直线与x轴的正半轴的夹角为30°,y2=$\frac{\sqrt{3}}{x}$(x>0)的图象如图所示,则下列结论正确的是( )
 已知直线OA的解析式为y1=kx,且这条直线与x轴的正半轴的夹角为30°,y2=$\frac{\sqrt{3}}{x}$(x>0)的图象如图所示,则下列结论正确的是( )
已知直线OA的解析式为y1=kx,且这条直线与x轴的正半轴的夹角为30°,y2=$\frac{\sqrt{3}}{x}$(x>0)的图象如图所示,则下列结论正确的是( )| A. | 两函数图象的交点坐标为($\sqrt{3}$,1)或(-$\sqrt{3}$,-1) | |
| B. | 当x>$\sqrt{3}$时,y2>y1 | |
| C. | 当x=1时,BC=2$\sqrt{3}$ | |
| D. | 当x=1时,△ABC的面积为1-$\frac{\sqrt{3}}{3}$ |
15.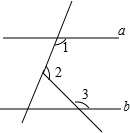 如图,a∥b,∠1=115°,∠2=95°,则∠3为( )
如图,a∥b,∠1=115°,∠2=95°,则∠3为( )
 如图,a∥b,∠1=115°,∠2=95°,则∠3为( )
如图,a∥b,∠1=115°,∠2=95°,则∠3为( )| A. | 120° | B. | 135° | C. | 150° | D. | 145° |
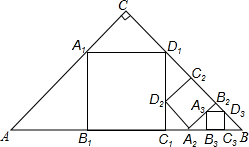 如图,△ABC,∠C=90°,AC=BC=a,在△ABC中截出一个正方形A1B1C1D1,使点A1,D1分别在AC,BC边上,边B1C1在AB边上;在△BC1D1在截出第二个正方形A2B2C2D2,使点A2,D2分别在BC1,D1C1边上,边B2C2在BD1边上;…,依此方法作下去,则第n个正方形的边长为($\frac{\sqrt{2}}{3}$)na.
如图,△ABC,∠C=90°,AC=BC=a,在△ABC中截出一个正方形A1B1C1D1,使点A1,D1分别在AC,BC边上,边B1C1在AB边上;在△BC1D1在截出第二个正方形A2B2C2D2,使点A2,D2分别在BC1,D1C1边上,边B2C2在BD1边上;…,依此方法作下去,则第n个正方形的边长为($\frac{\sqrt{2}}{3}$)na.