题目内容
8.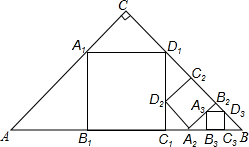 如图,△ABC,∠C=90°,AC=BC=a,在△ABC中截出一个正方形A1B1C1D1,使点A1,D1分别在AC,BC边上,边B1C1在AB边上;在△BC1D1在截出第二个正方形A2B2C2D2,使点A2,D2分别在BC1,D1C1边上,边B2C2在BD1边上;…,依此方法作下去,则第n个正方形的边长为($\frac{\sqrt{2}}{3}$)na.
如图,△ABC,∠C=90°,AC=BC=a,在△ABC中截出一个正方形A1B1C1D1,使点A1,D1分别在AC,BC边上,边B1C1在AB边上;在△BC1D1在截出第二个正方形A2B2C2D2,使点A2,D2分别在BC1,D1C1边上,边B2C2在BD1边上;…,依此方法作下去,则第n个正方形的边长为($\frac{\sqrt{2}}{3}$)na.
分析 设正方形A1B1C1D1的边长为x,利用△CA1D1和△AA1B1都是等腰直角三角形得到A1C=$\frac{\sqrt{2}}{2}$x,AA1=$\sqrt{2}$x,则$\frac{\sqrt{2}}{2}$x+$\sqrt{2}$x=a,解得x=$\frac{\sqrt{2}}{3}$a,于是得第1个正方形的边长为$\frac{\sqrt{2}}{3}$a,运用同样的方法可得第2个正方形的边长为($\frac{\sqrt{2}}{3}$)2a,于是根据指数与序号的关系可得第n个正方形的边长为($\frac{\sqrt{2}}{3}$)na.
解答 解:设正方形A1B1C1D1的边长为x,
∵△CA1D1和△AA1B1都是等腰直角三角形,
∴A1C=$\frac{\sqrt{2}}{2}$x,AA1=$\sqrt{2}$x,
∴$\frac{\sqrt{2}}{2}$x+$\sqrt{2}$x=a,解得x=$\frac{\sqrt{2}}{3}$a,
即第1个正方形的边长为$\frac{\sqrt{2}}{3}$a,
设正方形A2B2C2D2的边长为y,
∵△C2D1D2和△C1A2D2都是等腰直角三角形,
∴C1D2=$\frac{\sqrt{2}}{2}$y,D1D2=$\sqrt{2}$y,
∴$\frac{\sqrt{2}}{2}$y+$\sqrt{2}$y=$\frac{\sqrt{2}}{3}$a,解得y=($\frac{\sqrt{2}}{3}$)2a,
即第2个正方形的边长为($\frac{\sqrt{2}}{3}$)2a,
同理可得第3个正方形的边长为($\frac{\sqrt{2}}{3}$)3a,
∴第n个正方形的边长为($\frac{\sqrt{2}}{3}$)na.
故答案为($\frac{\sqrt{2}}{3}$)na.
点评 本题考查了等腰直角三角形的性质和正方形的性质,灵活应用等腰直角三角形三边的关系进行几何计算.

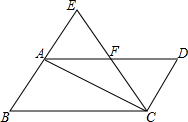 如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )
如图,在平行四边形ABCD中,∠B=60°,将△ABC沿对角线AC折叠,点B的对应点落在点E处,且点B,A,E在一条直线上,CE交AD于点F,则图中等边三角形共有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
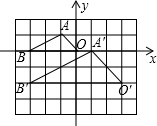 如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )
如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )| A. | (0,0) | B. | (0,1) | C. | (-3,2) | D. | (3,-2) |
| A. | -1 | B. | 1 | C. | -3 | D. | 5 |
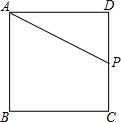 如图所示,若正方形ABCD的边长为2,P为DC上一动点.设DP=x,求△APD的面积y与x之间的函数关系式,并画出函数的图象.
如图所示,若正方形ABCD的边长为2,P为DC上一动点.设DP=x,求△APD的面积y与x之间的函数关系式,并画出函数的图象.