题目内容
8.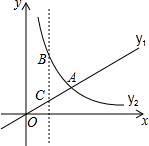 已知直线OA的解析式为y1=kx,且这条直线与x轴的正半轴的夹角为30°,y2=$\frac{\sqrt{3}}{x}$(x>0)的图象如图所示,则下列结论正确的是( )
已知直线OA的解析式为y1=kx,且这条直线与x轴的正半轴的夹角为30°,y2=$\frac{\sqrt{3}}{x}$(x>0)的图象如图所示,则下列结论正确的是( )| A. | 两函数图象的交点坐标为($\sqrt{3}$,1)或(-$\sqrt{3}$,-1) | |
| B. | 当x>$\sqrt{3}$时,y2>y1 | |
| C. | 当x=1时,BC=2$\sqrt{3}$ | |
| D. | 当x=1时,△ABC的面积为1-$\frac{\sqrt{3}}{3}$ |
分析 作AD⊥x轴于D,如图,设A(t,$\frac{\sqrt{3}}{t}$)(t>0),在Rt△OAD中,根据正切的定义可得$\frac{\frac{\sqrt{3}}{t}}{t}$=$\frac{\sqrt{3}}{3}$,解得t=$\sqrt{3}$,则两函数图象的交点坐标为A($\sqrt{3}$,1),反比例函数图象只在第一象限,于是可对A进行判断;观察函数图象,当x>$\sqrt{3}$时,一次函数图象都在反比例函数图象的上方,则可对B进行判断;利用待定系数法求出OA的解析式为y=$\frac{\sqrt{3}}{3}$x,则易得B(1,$\sqrt{3}$)和C(1,$\frac{\sqrt{3}}{3}$),于是计算出BC的长,则可对C进行判断;根据三角形面积公式可对D进行判断.
解答 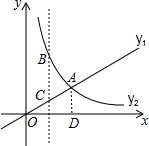 解:作AD⊥x轴于D,如图,
解:作AD⊥x轴于D,如图,
设A(t,$\frac{\sqrt{3}}{t}$)(t>0),
在Rt△OAD中,∵tan∠AOD=tan30°=$\frac{\frac{\sqrt{3}}{t}}{t}$=$\frac{\sqrt{3}}{3}$,
∴t=$\sqrt{3}$,
∴A($\sqrt{3}$,1),所以A选项错误;
当x>$\sqrt{3}$时,y1>y2,所以B选项错误;
把A($\sqrt{3}$,1)代入y=kx得k=$\frac{\sqrt{3}}{3}$,则直线OA的解析式为y=$\frac{\sqrt{3}}{3}$x,
当x=1时,y=$\frac{\sqrt{3}}{x}$=$\sqrt{3}$,则B(1,$\sqrt{3}$);当x=1时,y=$\frac{\sqrt{3}}{3}$x=$\frac{\sqrt{3}}{3}$,则C(1,$\frac{\sqrt{3}}{3}$),
∴BC=$\sqrt{3}$-$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$,所以C选项错误;
S△ABC=$\frac{1}{2}$×($\sqrt{3}$-1)×$\frac{2\sqrt{3}}{3}$=1-$\frac{\sqrt{3}}{3}$,所以D选项正确.
故选D.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了三角形面积公式.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案| A. | -1 | B. | 1 | C. | -3 | D. | 5 |
| A. | a2•a3=a6 | B. | (a3)2=a5 | C. | (3ab2)3=9a3b6 | D. | a6÷a2=a4 |
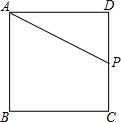 如图所示,若正方形ABCD的边长为2,P为DC上一动点.设DP=x,求△APD的面积y与x之间的函数关系式,并画出函数的图象.
如图所示,若正方形ABCD的边长为2,P为DC上一动点.设DP=x,求△APD的面积y与x之间的函数关系式,并画出函数的图象.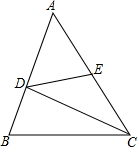 如图,在△ABC中,E点为AC的中点,其中BD=1,DC=3,BC=$\sqrt{10}$,AD=$\sqrt{7}$,求DE的长.
如图,在△ABC中,E点为AC的中点,其中BD=1,DC=3,BC=$\sqrt{10}$,AD=$\sqrt{7}$,求DE的长.