题目内容
12.在?ABCD中,BC边上的高为4,AB=5,AC=2$\sqrt{5}$,求?ABCD的周长.分析 根据题意分别画出图形,BC边上的高在平行四边形的内部和外部,进而利用勾股定理求出即可.
解答  解:如图1所示:
解:如图1所示:
∵在?ABCD中,BC边上的高为4,AB=5,AC=2$\sqrt{5}$,
∴EC=$\sqrt{{AC}^{2}{-AE}^{2}}$=2,AB=CD=5,
BE=$\sqrt{{AB}^{2}{-AE}^{2}}$=3,
∴AD=BC=5,
∴?ABCD的周长等于:20,
如图2所示:
∵在?ABCD中,BC边上的高为4,AB=5,AC=2$\sqrt{5}$,
∴EC=$\sqrt{{{AC}^{2}-AE}^{2}}$=2,AB=CD=5,
BE=3,
∴BC=3-2=1,
∴?ABCD的周长等于:1+1+5+5=12,
则?ABCD的周长等于12或20.
点评 此题主要考查了平行四边形的性质以及勾股定理等知识,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
3.已知m+n=2,mn=-2,则(1-m)(1-n)的值为( )
| A. | -1 | B. | 1 | C. | -3 | D. | 5 |
20.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (a3)2=a5 | C. | (3ab2)3=9a3b6 | D. | a6÷a2=a4 |
4.若等腰三角形的周长为20,有一边长为4,则它的腰长为( )
| A. | 4 | B. | 8 | C. | 10 | D. | 4或8 |
2.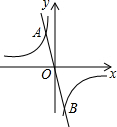 如图,反比例反数y=$\frac{{k}_{1}}{x}$与正比例函数y=k2x的图象交于A(-2,4),B两点,若$\frac{{k}_{1}}{x}$>k2x,则x的取值范围是( )
如图,反比例反数y=$\frac{{k}_{1}}{x}$与正比例函数y=k2x的图象交于A(-2,4),B两点,若$\frac{{k}_{1}}{x}$>k2x,则x的取值范围是( )
 如图,反比例反数y=$\frac{{k}_{1}}{x}$与正比例函数y=k2x的图象交于A(-2,4),B两点,若$\frac{{k}_{1}}{x}$>k2x,则x的取值范围是( )
如图,反比例反数y=$\frac{{k}_{1}}{x}$与正比例函数y=k2x的图象交于A(-2,4),B两点,若$\frac{{k}_{1}}{x}$>k2x,则x的取值范围是( )| A. | -2<x<0 | B. | -2<x<2 | C. | -2<x<0或x>2 | D. | x<-2或0<x<2 |
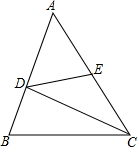 如图,在△ABC中,E点为AC的中点,其中BD=1,DC=3,BC=$\sqrt{10}$,AD=$\sqrt{7}$,求DE的长.
如图,在△ABC中,E点为AC的中点,其中BD=1,DC=3,BC=$\sqrt{10}$,AD=$\sqrt{7}$,求DE的长.