题目内容
15.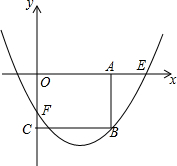 如图,在平面直角坐标系中,抛物线y=$\frac{1}{a}{x}^{2}-\frac{4}{a}x-a$(a>0)与x轴正半轴交于点E,与y轴交于点F,过点A(2a,0)作AB∥y轴,交抛物线于点B,过点B作BC⊥y轴于点C.
如图,在平面直角坐标系中,抛物线y=$\frac{1}{a}{x}^{2}-\frac{4}{a}x-a$(a>0)与x轴正半轴交于点E,与y轴交于点F,过点A(2a,0)作AB∥y轴,交抛物线于点B,过点B作BC⊥y轴于点C.(1)直接写出抛物线的对称轴;
(2)当点A在线段OE上时,求四边形OABC的面积的最大值;
(3)当四边形OABC为正方形时,求a的值.
分析 (1)根据对称轴公式可以直接求得抛物线的对称轴,本题得以解决;
(2)根据题意可以分别用含a的代数式表示出OA、AB的长,从而可以表示出四边形OABC的面积,进而可以取得面积的最大值;
(3)根据题意,可知OA=AB,由(2)中的OA与OB,可以求得a的值.
解答 解:(1)∵y=$\frac{1}{a}{x}^{2}-\frac{4}{a}x-a$(a>0),
∴对称轴为:x=$-\frac{-\frac{4}{a}}{2×\frac{1}{a}}=2$,
即抛物线的对称轴是x=2;
(2)将x=2a代入抛物线y=$\frac{1}{a}{x}^{2}-\frac{4}{a}x-a$(a>0),得y=3a-8,
∴S四边形OCBA=(8-3a)×2a=$-6(a-\frac{4}{3})^{2}+\frac{32}{3}$,
∴当a=$\frac{4}{3}$时,四边形OABC的面积求得最大值为$\frac{32}{3}$;
(3)当四边形OABC为正方形时,
2a=8-3a
解得a=$\frac{8}{5}$,
即当四边形OABC为正方形时,a的值是$\frac{8}{5}$.
点评 本题考查抛物线与x轴的交点,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
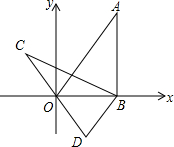 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为(-1,$\sqrt{3}$).
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为(-1,$\sqrt{3}$).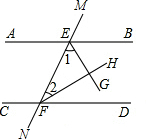 如图,直线AB和CD被直线MN所截,EG平分∠BEF,FH平分∠DFE,问:当∠1与∠2互余时,AB与CD有什么位置关系?为什么?
如图,直线AB和CD被直线MN所截,EG平分∠BEF,FH平分∠DFE,问:当∠1与∠2互余时,AB与CD有什么位置关系?为什么?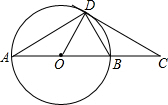 如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,DC与AB的延长线交于点C,∠A=30°,给出下面3个结论:∠BDC=∠A;AB=2BC;AD2=3BC2;其中正确结论的个数是( )
如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,DC与AB的延长线交于点C,∠A=30°,给出下面3个结论:∠BDC=∠A;AB=2BC;AD2=3BC2;其中正确结论的个数是( ) ?AOBC如图放置,A(1,2),B(2,0),先将平行四边形向左平移6个单位长度,再向下平移1个单位长度,然后沿x轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为(-1,3)或(1,-3).
?AOBC如图放置,A(1,2),B(2,0),先将平行四边形向左平移6个单位长度,再向下平移1个单位长度,然后沿x轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为(-1,3)或(1,-3).