题目内容
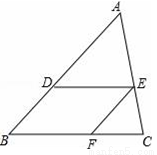
2.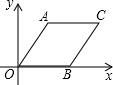 ?AOBC如图放置,A(1,2),B(2,0),先将平行四边形向左平移6个单位长度,再向下平移1个单位长度,然后沿x轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为(-1,3)或(1,-3).
?AOBC如图放置,A(1,2),B(2,0),先将平行四边形向左平移6个单位长度,再向下平移1个单位长度,然后沿x轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为(-1,3)或(1,-3).
分析 根据菱形的对称性求出点B的坐标,再求出AB的中点的坐标,进而求出点C的坐标,根据向左平移横坐标减,向下平移纵坐标减求出平移后的C点对应的坐标,结合翻折变换知识求出沿x轴翻折后C点对应的坐标,再根据旋转的性质确定点P的坐标.
解答 解:∵A(1,2),B(2,0),
∴点C坐标为(3,2),
∵向左平移6个单位长度,再向下平移1个单位长度,
∴3-6=-3,2-1=1,
∴平移后点C对应的坐标为(-3,1),
沿x轴翻折后C点对应的坐标为(-3,-1),
∵在坐标平面内绕点O旋转90°,
∴若是顺时针旋转,则对应点在第二象限,坐标为(-1,3),
若是逆时针旋转,则对应点在第四象限,坐标为(1,-3),
综上所述,点P的坐标为(-1,3)或(1,-3),
故答案为(-1,3)或(1,-3).
点评 本题考查了菱形的性质,坐标与图形的变化,熟练掌握菱形的性质以及平移、旋转变换的性质是解题的关键.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
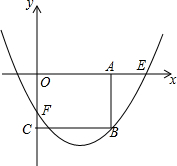 如图,在平面直角坐标系中,抛物线y=$\frac{1}{a}{x}^{2}-\frac{4}{a}x-a$(a>0)与x轴正半轴交于点E,与y轴交于点F,过点A(2a,0)作AB∥y轴,交抛物线于点B,过点B作BC⊥y轴于点C.
如图,在平面直角坐标系中,抛物线y=$\frac{1}{a}{x}^{2}-\frac{4}{a}x-a$(a>0)与x轴正半轴交于点E,与y轴交于点F,过点A(2a,0)作AB∥y轴,交抛物线于点B,过点B作BC⊥y轴于点C.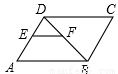
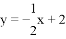 与
与 轴交于点B,与
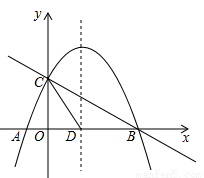
轴交于点B,与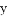 轴交于点C,已知二次函数的图象经过点B、C和点A(-1,0).
轴交于点C,已知二次函数的图象经过点B、C和点A(-1,0).