题目内容
7.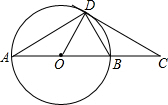 如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,DC与AB的延长线交于点C,∠A=30°,给出下面3个结论:∠BDC=∠A;AB=2BC;AD2=3BC2;其中正确结论的个数是( )
如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,DC与AB的延长线交于点C,∠A=30°,给出下面3个结论:∠BDC=∠A;AB=2BC;AD2=3BC2;其中正确结论的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 要想证明∠BDC=∠A,只要证明三角形ADB和三角形CDO的对应角相等即可;要想证明AB=2BC,只要证明BC等于半径即可;要证明AD2=3BC2只要说明AD、AB、BD之间的关系即可.
解答 解:∵AB是⊙O的直径,CD是⊙O的切线,切点为D,
∴∠ADB=∠ODC=90°,
∵∠A=30°,
∴∠DBO=60°,
∵OB=OD,
∴△OBD是等边三角形,
∴∠ODB=60°,
∠BDC=∠ADO,
又∵OA=OD,
∴∠A=∠ADO,
∴∠BDC=∠A;
∵∠ODC=90°,∠C=30°,
∴OC=2OD,
∴AB=2OC,BC=OA,
∴AB=2BC;
∵∠ADB=90°,∠A=30°,
∴AB=2BD,AD=$\sqrt{3}BD$,
∴AD2=3BD2,
即AD2=3BC2;
故选D.
点评 本题考查切线的性质,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
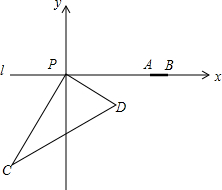 如图,在东西方向的海岸线l有一长为2km的码头AB,在码头的西端A的正西29km处有一观测站P,某时刻测得一艘匀速直线航行的轮船位于P的南偏西30°,且与P相距30km的C处;经过1小时40分钟,又测得该轮船位于P的南偏东60°,且与P相距10$\sqrt{3}$的D处.
如图,在东西方向的海岸线l有一长为2km的码头AB,在码头的西端A的正西29km处有一观测站P,某时刻测得一艘匀速直线航行的轮船位于P的南偏西30°,且与P相距30km的C处;经过1小时40分钟,又测得该轮船位于P的南偏东60°,且与P相距10$\sqrt{3}$的D处.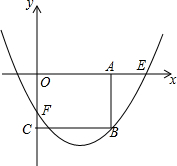 如图,在平面直角坐标系中,抛物线y=$\frac{1}{a}{x}^{2}-\frac{4}{a}x-a$(a>0)与x轴正半轴交于点E,与y轴交于点F,过点A(2a,0)作AB∥y轴,交抛物线于点B,过点B作BC⊥y轴于点C.
如图,在平面直角坐标系中,抛物线y=$\frac{1}{a}{x}^{2}-\frac{4}{a}x-a$(a>0)与x轴正半轴交于点E,与y轴交于点F,过点A(2a,0)作AB∥y轴,交抛物线于点B,过点B作BC⊥y轴于点C.