题目内容
14.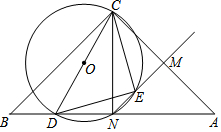 已知△ABC中,∠BCA=90°,BC=AC,D是BA边上一点(点D不与A,B重合),M是CA中点,当以CD为直径的⊙O与BA边交于点N,⊙O与射线NM交于点E,连接CE,DE.
已知△ABC中,∠BCA=90°,BC=AC,D是BA边上一点(点D不与A,B重合),M是CA中点,当以CD为直径的⊙O与BA边交于点N,⊙O与射线NM交于点E,连接CE,DE.(1)求证:BN=AN;
(2)猜想线段CD与DE的数量关系,并说明理由.
分析 (1)根据圆周角定理求出∠CND=90°,根据等腰三角形的性质得出即可;
(2)根据直角三角形斜边上中线性质求出CN=AN,根据等腰三角形性质求出∠CNM=45°,根据圆周角定理求出∠CED=90°,∠CDE=∠CNE=45°,根据勾股定理求出即可.
解答 (1)证明:∵CD为⊙O的直径,
∴∠CND=90°,
∴CN⊥AB,
∵BC=AC,
∴BN=AN;
(2)解:CD=$\sqrt{2}$DE,
理由如下:∵△ABC中,∠BCA=90°,BN=AN,
∴CN=AN,
∵点M是CA中点,
∴NM平分∠CNA,
∵∠CNA=90°,
∴∠CNM=45°,
∴∠CDE=∠CNE=45°,
∵CD为⊙O的直径,
∴∠CED=90°,
∴∠DCE=45°=∠CDE,
∴DE=CE,
∵CE2+DE2=CD2,
∴CD=$\sqrt{2}$DE.
点评 本题考查了勾股定理,等腰三角形的性质,直角三角形斜边上中线性质,圆周角定理等知识点,能综合运用定理进行推理是解此题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
4.二次函数y=(x+3)2+7的顶点坐标是( )
| A. | (-3,7) | B. | (3,7) | C. | (-3,-7) | D. | (3,-7) |
9.用配方法解关于x的一元二次方程x2-2x-3=0,配方后的方程可以是( )
| A. | (x+1)2=4 | B. | (x-1)2=4 | C. | (x-1)2=2 | D. | (x+1)2=2 |
19.在平面直角坐标系中,有A(1,2),B(4,3)两点,现另取一点C(a,1),满足:AC+BC的值最小.则a的值为( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 3 |
