题目内容
2．解下列方程（1）2x+1=4x-2
（2）$\frac{3y-6}{4}$=1-$\frac{5y-7}{3}$．
分析 （1）方程移项合并，把x系数化为1，即可求出解；
（2）方程去分母，去括号，移项合并，把y系数化为1，即可求出解．
解答 解：（1）移项，得2x-4x=-2-1，
合并同类项，得-2x=-3，
系数化为1，得x=1.5；
（2）去分母，得3（3y-6）=12-4（5y-7），
去括号，得9y-18=12-20y+28，
移项，得9y+20y=12+28+18，
合并同类项，得29y=58，
系数化为1，得y=2．
点评 此题考查了解一元一次方程，去分母时注意方程各项都乘以各分母的最小公倍数．
练习册系列答案
相关题目
12．
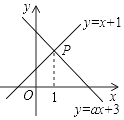如图，已知函数y=x+1和y=ax+3图象交于点P，点P的横坐标为1，则关于x，y的方程组$\left\{\begin{array}{l}{x-y=-1}\\{ax-y=-3}\end{array}\right.$的解是（ ）
如图，已知函数y=x+1和y=ax+3图象交于点P，点P的横坐标为1，则关于x，y的方程组$\left\{\begin{array}{l}{x-y=-1}\\{ax-y=-3}\end{array}\right.$的解是（ ）| A． | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ |
如图，将一直角三角板与两边平行的纸条如图所示放置，下列结论：①∠1=∠2 ②∠3=∠4 ③∠4+∠5=180° ④∠2+∠3=90°
7．下列几何图形中既是中心对称图形，又是轴对称图形的是（ ）
| A． | 圆 | B． | 正五边形 | C． | 平行四边形 | D． | 等边三角形 |
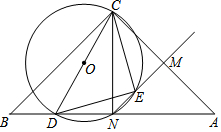已知△ABC中，∠BCA=90°，BC=AC，D是BA边上一点（点D不与A，B重合），M是CA中点，当以CD为直径的⊙O与BA边交于点N，⊙O与射线NM交于点E，连接CE，DE．