题目内容
15.在平面直角坐标系中,若二次函数y=ax2+bc+c的图象的顶点为M,且图象经过A(0,4),B(4,4)两点,若M到线段AB的距离为4,则a的值为-1.分析 由抛物线的对称性得出对称轴为x=2,由M到线段AB的距离为4得出顶点纵坐标,据此可得抛物线的顶点坐标,待定系数法求解得出a的值.
解答 解:∵图象经过A(0,4),B(4,4)两点,
∴抛物线的对称轴为x=2,
∵M到线段AB的距离为4,
∴顶点M到x轴的距离为4+4=8,即顶点纵坐标为8,
∴抛物线的顶点坐标为(2,8),
设抛物线解析式为y=a(x-2)2+8,
将点A(0,4)代入,得:4a+8=4,
解得:a=-1,
故答案为:-1.
点评 本题主要考查二次函数的性质及二次函数图象上点的坐标特征,熟练掌握抛物线的对称性得出顶点坐标是解题的关键.

练习册系列答案
相关题目
19.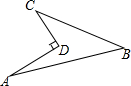 如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为( )平方米.
如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为( )平方米.
 如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为( )平方米.
如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为( )平方米.| A. | 96 | B. | 204 | C. | 196 | D. | 304 |




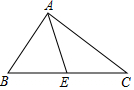 如图,△ABC中,AC=$\sqrt{3}$,AB=$\sqrt{2}$,E是边BC的中点,且AE=$\frac{\sqrt{5}}{2}$,求证:△ABC是直角三角形.
如图,△ABC中,AC=$\sqrt{3}$,AB=$\sqrt{2}$,E是边BC的中点,且AE=$\frac{\sqrt{5}}{2}$,求证:△ABC是直角三角形.