题目内容
5.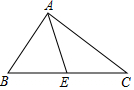 如图,△ABC中,AC=$\sqrt{3}$,AB=$\sqrt{2}$,E是边BC的中点,且AE=$\frac{\sqrt{5}}{2}$,求证:△ABC是直角三角形.
如图,△ABC中,AC=$\sqrt{3}$,AB=$\sqrt{2}$,E是边BC的中点,且AE=$\frac{\sqrt{5}}{2}$,求证:△ABC是直角三角形.
分析 作CF平行于AB交AE的延长线于F,首先证明△AEB≌△FEC,可得AE=FE=$\frac{\sqrt{5}}{2}$,AB=FC=$\sqrt{2}$,再利用勾股定理逆定理可证明∠ACF=90°,再根据平行线的性质可得∠CAB=90°,从而证明△ABC是直角三角形.
解答 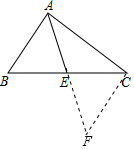 证明:如图,作CF平行于AB交AE的延长线于F,
证明:如图,作CF平行于AB交AE的延长线于F,
∵E是边BC的中点,
∴BE=CE,
∵CF∥AB,
∴∠B=∠ECF,
在△AEB与△FEC中,
$\left\{\begin{array}{l}{∠B=∠ECF}\\{BE=CE}\\{∠AEB=∠FEC}\end{array}\right.$,
∴△AEB≌△FEC(ASA),
∴AE=FE=$\frac{\sqrt{5}}{2}$,AB=FC=$\sqrt{2}$,
∴AF=$\sqrt{5}$,
∵AC=$\sqrt{3}$,
∵($\sqrt{2}$)2+($\sqrt{3}$)2=($\sqrt{5}$)2,
∴△AFC是直角三角形.
∴∠ACF=90°,
∵AE∥BC,
∴∠CAB=180°-∠ACF=90°,
∴△ABC是直角三角形.
点评 此题考查了勾股定理的逆定理,全等三角形的判定与性质,平行线的性质,关键是正确画出辅助线,证明△AFC是直角三角形.

练习册系列答案
相关题目
13.下列图形中,有且只有2条对称轴的是( )
| A. |  | B. |  | C. |  | D. |  |
20.一次函数y=3x+5的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.下列说法正确的是( )
| A. | 相等的两个角是对顶角 | |
| B. | 同位角相等 | |
| C. | 图形平移后的大小可以发生改变 | |
| D. | 两条直线相交所成的四个角都相等,则这两条直线互相垂直 |
17.下列式子正确的是( )
| A. | $\sqrt{25}$=±5 | B. | $\root{3}{-7}$=-$\root{3}{7}$ | C. | ±$\sqrt{64}$=8 | D. | $\sqrt{(-5)^{2}}$=-5 |
 已知甲、乙两地相距90km,A、B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE、OC分别表示A、B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题:
已知甲、乙两地相距90km,A、B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE、OC分别表示A、B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题: