题目内容
3.已知二次函数y=a(x+1)2-b(a≠0)有最小值1,则$\sqrt{{a}^{2}}$-|a-3b|=3.分析 根据函数有最小值判断出a的符号,进而由最小值求出b,把a、b代入代数式可得出结论.
解答 解:∵二次函数y=a(x+1)2-b(a≠0)有最小值,
∴抛物线开口方向向上,即a>0;
又最小值为1,即-b=1,
∴b=-1,
∴$\sqrt{{a}^{2}}$-|a-3b|=a-a+3=3,
故答案为:3.
点评 本题考查的是二次函数的最值,求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.

练习册系列答案
相关题目
7.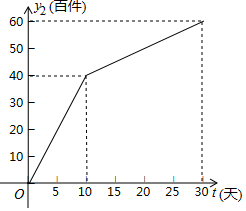 我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.
我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映y1与t的变化规律,并求出y1与t的函数关系式及自变量t的取值范围;
(2)求y2与t的函数关系式,并写出自变量t的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为y(百件),求y与t的函数关系式;当t为何值时,日销售总量y达到最大,并求出此时的最大值.
 我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.
我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.| 时间t(天) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 日销售量 y1(百件) | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
(2)求y2与t的函数关系式,并写出自变量t的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为y(百件),求y与t的函数关系式;当t为何值时,日销售总量y达到最大,并求出此时的最大值.
11.将函数y=-3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )
| A. | y=-3x+2 | B. | y=-3x-2 | C. | y=-3(x+2) | D. | y=-3(x-2) |
12.在同一坐标系中,抛物线y=x2,y=-x2,y=$\frac{1}{2}$x2的共同点是( )
| A. | 开口向上,对称轴是y轴,顶点是原点 | |
| B. | 开口向下,对称轴是y轴,顶点是原点 | |
| C. | 对称轴是y轴,顶点是原点 | |
| D. | 函数y的最小值为0 |
13.下列图形中,有且只有2条对称轴的是( )
| A. |  | B. |  | C. |  | D. |  |