题目内容
6.方程组$\left\{\begin{array}{l}{y-\sqrt{x-2}=0}\\{x-ky+2k+10=0}\end{array}\right.$中,方程组只有一组解,则k=23或-1.分析 ①•k+②得,得到x2+(18+2k)x+40k+104=0,由于方程组只有一组解,得到△=(18+2k)2-4(40k+104)=0,即可得到结论.
解答 解:$\left\{\begin{array}{l}{y-\sqrt{x-2}=0①}\\{x-ky+2k+10=0②}\end{array}\right.$,
①•k+②得,x-2$\sqrt{x-2}$+2k+10=0,
即x2+(18+2k)x+40k+104=0,
∵方程组只有一组解,
∴△=(18+2k)2-4(40k+104)=0,
∴k=23或k=-1,
故答案为:23或-1.
点评 本题考查了解二元一次方程组,一元二次方程根的判别式,熟练掌握二元一次方程组的解法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.将函数y=-3x的图象沿y轴向上平移2个单位长度后,所得图象对应的函数关系式为( )
| A. | y=-3x+2 | B. | y=-3x-2 | C. | y=-3(x+2) | D. | y=-3(x-2) |
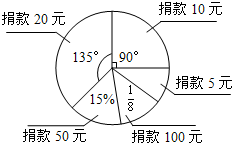 在抗震救灾的捐款活动中,六(2)班同学的捐款人数情况如图所示,其中捐款10元的人数为10人.请根据图象回答下列问题:
在抗震救灾的捐款活动中,六(2)班同学的捐款人数情况如图所示,其中捐款10元的人数为10人.请根据图象回答下列问题: