题目内容
19．
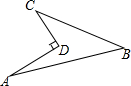如图所示的一块地，已知∠ADC=90°，AD=12m，CD=9m，AB=25m，BC=20m，则这块地的面积为（ ）平方米．| A． | 96 | B． | 204 | C． | 196 | D． | 304 |
分析 连接AC，先利用勾股定理求出AC，再根据勾股定理的逆定理判定△ABC是直角三角形，那么△ABC的面积减去△ACD的面积就是所求的面积．
解答 解：如图，连接AC．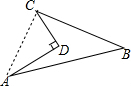
在△ACD中，∵AD=12m，CD=9m，∠ADC=90°，
∴AC=15m，
又∵AC2+BC2=152+202=252=AB2，
∴△ABC是直角三角形，
∴这块地的面积=△ABC的面积-△ACD的面积=$\frac{1}{2}$×15×20-$\frac{1}{2}$×9×12=96（平方米）．
故选A．
点评 本题考查了勾股定理、勾股定理的逆定理的应用，得到△ABC是直角三角形是解题的关键．同时考查了直角三角形的面积公式．
练习册系列答案
相关题目
7．
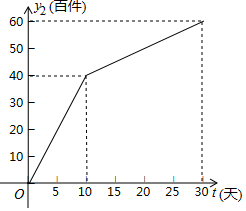我市雷雷服饰有限公司生产了一款夏季服装，通过实体商店和网上商店两种途径进行销售，销售一段时间后，该公司对这种商品的销售情况，进行了为期30天的跟踪调查，其中实体商店的日销售量y1（百件）与时间t（t为整数，单位：天）的部分对应值如表所示，网上商店的日销售量y2（百件）与时间t（t为整数，单位：天）的部分对应值如图所示．
（1）请你在一次函数、二次函数和反比例函数中，选择合适的函数能反映y1与t的变化规律，并求出y1与t的函数关系式及自变量t的取值范围；
（2）求y2与t的函数关系式，并写出自变量t的取值范围；
（3）在跟踪调查的30天中，设实体商店和网上商店的日销售总量为y（百件），求y与t的函数关系式；当t为何值时，日销售总量y达到最大，并求出此时的最大值．
我市雷雷服饰有限公司生产了一款夏季服装，通过实体商店和网上商店两种途径进行销售，销售一段时间后，该公司对这种商品的销售情况，进行了为期30天的跟踪调查，其中实体商店的日销售量y1（百件）与时间t（t为整数，单位：天）的部分对应值如表所示，网上商店的日销售量y2（百件）与时间t（t为整数，单位：天）的部分对应值如图所示．| 时间t（天） | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 日销售量 y1（百件） | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
（2）求y2与t的函数关系式，并写出自变量t的取值范围；
（3）在跟踪调查的30天中，设实体商店和网上商店的日销售总量为y（百件），求y与t的函数关系式；当t为何值时，日销售总量y达到最大，并求出此时的最大值．
14．
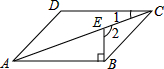如图，在?ABCD中，BE⊥AB交对角线AC于点E，若∠2=110°，则∠1=（ ）
如图，在?ABCD中，BE⊥AB交对角线AC于点E，若∠2=110°，则∠1=（ ）| A． | 40° | B． | 30° | C． | 25° | D． | 20° |
4．下列各组数中互为相反数的是（ ）
| A． | -2与-$\frac{1}{2}$ | B． | 2与|-2| | C． | -2与$\root{3}{-8}$ | D． | -2与$\sqrt{（-2）^{2}}$ |